Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 490 Атанасян — Подробные Ответы
Стороны оснований правильной усечённой треугольной пирамиды равны \(a\) и \(0,5a\), апофема боковой грани равна \(a\). Найдите объём усечённой пирамиды.
Площади оснований правильной усечённой треугольной пирамиды равны \(S_1 = \frac{a^2 \sqrt{3}}{4}\) и \(S_2 = \frac{(a/2)^2 \sqrt{3}}{4} = \frac{a^2 \sqrt{3}}{16}\). Радиусы вписанных окружностей оснований равны \(r_1 = \frac{a}{2\sqrt{3}}\) и \(r_2 = \frac{a/2}{2\sqrt{3}} = \frac{a}{4\sqrt{3}}\). Высота усечённой пирамиды \(h\) связана с апофемой боковой грани \(a\) соотношением \(h^2 + (r_1 — r_2)^2 = a^2\). Подставляя значения, получаем \(h^2 + (\frac{a}{2\sqrt{3}} — \frac{a}{4\sqrt{3}})^2 = a^2\), что приводит к \(h^2 + (\frac{a}{4\sqrt{3}})^2 = a^2\), далее \(h^2 + \frac{a^2}{48} = a^2\). Отсюда \(h^2 = \frac{47a^2}{48}\), и \(h = a \sqrt{\frac{47}{48}}\). Объём усечённой пирамиды равен \(V = \frac{1}{3} h (S_1 + S_2 + \sqrt{S_1 S_2})\). Подставляя найденные значения \(h\), \(S_1\), \(S_2\) и \(\sqrt{S_1 S_2} = \sqrt{\frac{a^2 \sqrt{3}}{4} \cdot \frac{a^2 \sqrt{3}}{16}} = \frac{a^2 \sqrt{3}}{8}\), получаем \(V = \frac{1}{3} a \sqrt{\frac{47}{48}} (\frac{a^2 \sqrt{3}}{4} + \frac{a^2 \sqrt{3}}{16} + \frac{a^2 \sqrt{3}}{8})\). Упрощая выражение, находим \(V = \frac{a \sqrt{47}}{12\sqrt{3}} a^2 \sqrt{3} (\frac{4+1+2}{16}) = \frac{a^3 \sqrt{47}}{12} (\frac{7}{16}) = \frac{7 a^3 \sqrt{47}}{192}\).
Ответ: \(V_{ABCA_1B_1C_1} = \frac{7\sqrt{47}}{192} a^3\).
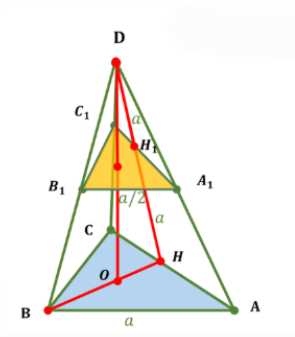
Дано: правильная усечённая треугольная пирамида \(ABCA_1B_1C_1\), основание \(ABC\) — правильный треугольник, \(AB = a\), \(A_1B_1 = a/2\), апофема усечённой пирамиды \(HH_1 = a\). Найти объём \(V_{ABCA_1B_1C_1}\).
Решение: Для нахождения объёма усечённой пирамиды можно достроить её до полной пирамиды \(DABC\), где \(D\) — вершина. Усечённая пирамида получается отсечением меньшей подобной пирамиды \(DA_1B_1C_1\) от полной пирамиды \(DABC\). Объём усечённой пирамиды равен разности объёмов полной и меньшей пирамид: \(V_{ABCA_1B_1C_1} = V_{DABC} — V_{DA_1B_1C_1}\).
Основания пирамид \(DABC\) и \(DA_1B_1C_1\) являются правильными треугольниками со сторонами \(a\) и \(a/2\) соответственно. Площадь правильного треугольника со стороной \(s\) равна \(S = \frac{s^2 \sqrt{3}}{4}\).
Площадь нижнего основания \(S_{\triangle ABC} = \frac{a^2 \sqrt{3}}{4}\).
Площадь верхнего основания \(S_{\triangle A_1B_1C_1} = \frac{(a/2)^2 \sqrt{3}}{4} = \frac{a^2/4 \sqrt{3}}{4} = \frac{a^2 \sqrt{3}}{16}\).
Пирамиды \(DABC\) и \(DA_1B_1C_1\) подобны с коэффициентом подобия по линейным размерам, равным отношению сторон оснований: \(k = \frac{A_1B_1}{AB} = \frac{a/2}{a} = \frac{1}{2}\). Отношение объёмов подобных тел равно кубу коэффициента подобия: \(\frac{V_{DA_1B_1C_1}}{V_{DABC}} = k^3 = (\frac{1}{2})^3 = \frac{1}{8}\).
Следовательно, \(V_{DA_1B_1C_1} = \frac{1}{8} V_{DABC}\).
Объём усечённой пирамиды равен \(V_{ABCA_1B_1C_1} = V_{DABC} — \frac{1}{8} V_{DABC} = \frac{7}{8} V_{DABC}\).
Объём полной пирамиды \(V_{DABC} = \frac{1}{3} S_{\triangle ABC} \cdot H\), где \(H\) — высота полной пирамиды \(DO\), а \(O\) — центр основания \(ABC\).
Чтобы найти высоту \(H\), рассмотрим прямоугольный треугольник, образованный высотой полной пирамиды \(DO\), радиусом вписанной окружности основания \(OH\), и апофемой полной пирамиды \(DH\). \(H\) — это \(DO\). \(OH\) — это радиус вписанной окружности правильного треугольника со стороной \(a\), который равен \(r = \frac{a}{2\sqrt{3}}\). Апофема полной пирамиды \(DH\) связана с апофемой усечённой пирамиды \(HH_1\) и коэффициентом подобия. Апофема меньшей пирамиды \(DH_1\) равна \(k \cdot DH = \frac{1}{2} DH\). Апофема усечённой пирамиды \(HH_1 = DH — DH_1 = DH — \frac{1}{2} DH = \frac{1}{2} DH\). Дано \(HH_1 = a\), следовательно, \(\frac{1}{2} DH = a\), откуда \(DH = 2a\).
Теперь в прямоугольном треугольнике \(DOH\) по теореме Пифагора: \(DO^2 + OH^2 = DH^2\).
\(DO^2 + (\frac{a}{2\sqrt{3}})^2 = (2a)^2\).
\(DO^2 + \frac{a^2}{12} = 4a^2\).
\(DO^2 = 4a^2 — \frac{a^2}{12} = \frac{48a^2 — a^2}{12} = \frac{47a^2}{12}\).
Высота полной пирамиды \(DO = \sqrt{\frac{47a^2}{12}} = a \sqrt{\frac{47}{12}}\).
Теперь подставим значение \(DO\) и \(S_{\triangle ABC}\) в формулу для объёма полной пирамиды:
\(V_{DABC} = \frac{1}{3} \cdot \frac{a^2 \sqrt{3}}{4} \cdot a \sqrt{\frac{47}{12}}\).
\(V_{DABC} = \frac{a^3 \sqrt{3} \sqrt{47}}{12 \sqrt{12}} = \frac{a^3 \sqrt{3 \cdot 47}}{12 \sqrt{4 \cdot 3}} = \frac{a^3 \sqrt{141}}{12 \cdot 2 \sqrt{3}} = \frac{a^3 \sqrt{3 \cdot 47}}{24 \sqrt{3}}\).
Умножим числитель и знаменатель на \(\sqrt{3}\):
\(V_{DABC} = \frac{a^3 \sqrt{3 \cdot 47} \cdot \sqrt{3}}{24 \sqrt{3} \cdot \sqrt{3}} = \frac{a^3 \sqrt{47} \cdot 3}{24 \cdot 3} = \frac{a^3 \sqrt{47}}{24}\).
Теперь найдём объём усечённой пирамиды:
\(V_{ABCA_1B_1C_1} = \frac{7}{8} V_{DABC} = \frac{7}{8} \cdot \frac{a^3 \sqrt{47}}{24} = \frac{7 a^3 \sqrt{47}}{192}\).
Ответ: \(V_{ABCA_1B_1C_1} = \frac{7\sqrt{47}}{192} a^3\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.