
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 489 Атанасян — Подробные Ответы
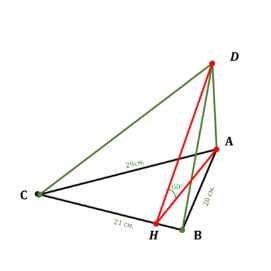
Основанием пирамиды \(DABC\) является треугольник, в котором \(АВ = 20\) см, \(АС = 29\) см, \(ВС = 21\) см. Грани \(DAB\) и \(DAC\) перпендикулярны к плоскости основания, а грань \(DBC\) составляет с ней угол в 60°. Найдите объём пирамиды.
Основание пирамиды — треугольник \(АВС\). Полупериметр треугольника \(p = \frac{AB+BC+AC}{2} = \frac{20+21+29}{2} = 35\) см. Площадь основания по формуле Герона \(S_{ABC} = \sqrt{p(p-AB)(p-BC)(p-AC)} = \sqrt{35(35-20)(35-21)}\)
\(\sqrt{(35-29)} = \sqrt{35 \cdot 15 \cdot 14 \cdot 6} = 210\) см². Так как грани \(DAB\) и \(DAC\) перпендикулярны основанию, высота пирамиды \(AD\) перпендикулярна плоскости основания. Проведем \(АН \perp ВС\). Тогда \(DH \perp BC\) по теореме о трех перпендикулярах, и угол \(\angle DHA\) является линейным углом двугранного угла при ребре \(ВС\), равным 60°. Площадь треугольника \(АВС\) также равна \(\frac{1}{2} \cdot BC \cdot AH\). Отсюда \(AH = \frac{2 \cdot S_{ABC}}{BC} = \frac{2 \cdot 210}{21} = 20\) см. В прямоугольном треугольнике \(ADH\), \(AD = AH \cdot \tan(\angle DHA) = 20 \cdot \tan(60^\circ) = 20\sqrt{3}\) см. Объем пирамиды \(V = \frac{1}{3} S_{ABC} \cdot AD = \frac{1}{3} \cdot 210 \cdot 20\sqrt{3} = 1400\sqrt{3}\) см³. Ответ: \(V_{пирамиды} = 1400\sqrt{3}\) см³.
Основанием данной пирамиды \(ABCD\) является треугольник \(ABC\). Известны длины сторон основания: \(AB = 20\) см, \(BC = 21\) см, \(AC = 29\) см.
Для начала найдем площадь основания \(S_{ABC}\). Поскольку известны длины всех трех сторон треугольника, можно использовать формулу Герона. Сначала вычислим полупериметр \(p\) треугольника \(ABC\):
\(p = \frac{AB + BC + AC}{2} = \frac{20 + 21 + 29}{2} = \frac{70}{2} = 35\) см.
Теперь применим формулу Герона для нахождения площади \(S_{ABC}\):
\(S_{ABC} = \sqrt{p(p — AB)(p — BC)(p — AC)} = \sqrt{35(35 — 20)(35 — 21)}\)
\(\sqrt{(35 — 29)} = \sqrt{35 \cdot 15 \cdot 14 \cdot 6}\).
Разложим числа под корнем на простые множители для упрощения:
\(35 = 5 \cdot 7\), \(15 = 3 \cdot 5\), \(14 = 2 \cdot 7\), \(6 = 2 \cdot 3\).
\(S_{ABC} = \sqrt{(5 \cdot 7) \cdot (3 \cdot 5) \cdot (2 \cdot 7) \cdot (2 \cdot 3)} = \sqrt{2^2 \cdot 3^2 \cdot 5^2 \cdot 7^2} = 2 \cdot 3 \cdot 5 \cdot 7 = \)
\(=210\) см².
Далее, нам дано, что грани \(ACD\) и \(ABD\) перпендикулярны плоскости основания \(ABC\). Если две плоскости перпендикулярны третьей плоскости, и они пересекаются по прямой, то эта прямая перпендикулярна третьей плоскости. В данном случае плоскости \(ACD\) и \(ABD\) пересекаются по прямой \(AD\), и обе они перпендикулярны плоскости основания \(ABC\). Следовательно, прямая \(AD\) перпендикулярна плоскости \(ABC\). Это означает, что \(AD\) является высотой пирамиды \(ABCD\).
Теперь рассмотрим грань \(DBC\). Угол между гранью \(DBC\) и плоскостью основания \(ABC\) равен 60°. Линейным углом двугранного угла между плоскостями \(DBC\) и \(ABC\) является угол между прямыми, проведенными в этих плоскостях перпендикулярно общей линии пересечения. Общей линией пересечения является ребро \(BC\). Проведем в плоскости основания \(ABC\) отрезок \(AH\) перпендикулярно \(BC\). Поскольку \(AD\) перпендикулярно плоскости \(ABC\), то \(AD\) перпендикулярно любой прямой в этой плоскости, в том числе \(BC\). У нас есть \(AH \perp BC\) (по построению) и \(AD \perp BC\) (так как \(AD\) — высота пирамиды). По теореме о трех перпендикулярах, если проекция наклонной (\(DH\)) на плоскость (\(ABC\)) перпендикулярна прямой в плоскости (\(BC\)), то и сама наклонная (\(DH\)) перпендикулярна этой прямой (\(BC\)). Таким образом, \(DH \perp BC\). Линейным углом двугранного угла при ребре \(BC\) является угол \(\angle DHA\), и по условию он равен 60°.
Теперь найдем длину отрезка \(AH\). Площадь треугольника \(ABC\) также может быть выражена через основание \(BC\) и высоту \(AH\), проведенную к этому основанию: \(S_{ABC} = \frac{1}{2} \cdot BC \cdot AH\).
Мы знаем \(S_{ABC} = 210\) см² и \(BC = 21\) см. Подставим эти значения в формулу:
\(210 = \frac{1}{2} \cdot 21 \cdot AH\).
Отсюда \(AH = \frac{2 \cdot 210}{21} = \frac{420}{21} = 20\) см.
Теперь рассмотрим прямоугольный треугольник \(ADH\). Угол \(\angle DHA = 60^\circ\), и \(AH = 20\) см. \(AD\) является противолежащим катетом к углу \(DHA\), а \(AH\) — прилежащим катетом. Используем тригонометрическую функцию тангенс:
\(\tan(\angle DHA) = \frac{AD}{AH}\).
\(\tan(60^\circ) = \frac{AD}{20}\).
Мы знаем, что \(\tan(60^\circ) = \sqrt{3}\).
\(\sqrt{3} = \frac{AD}{20}\).
Следовательно, \(AD = 20\sqrt{3}\) см. Это высота пирамиды.
Наконец, вычислим объем пирамиды \(V\). Формула объема пирамиды: \(V = \frac{1}{3} \cdot S_{основания} \cdot h\).
В нашем случае \(S_{основания} = S_{ABC} = 210\) см² и высота \(h = AD = 20\sqrt{3}\) см.
\(V = \frac{1}{3} \cdot 210 \cdot 20\sqrt{3}\).
\(V = 70 \cdot 20\sqrt{3} = 1400\sqrt{3}\) см³.
Объем пирамиды равен \(1400\sqrt{3}\) см³.
Ответ: \(V_{пирамиды} = 1400\sqrt{3}\) см³.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!