ГДЗ по Геометрии 11 класс Номер 488 Атанасян — Подробные Ответы

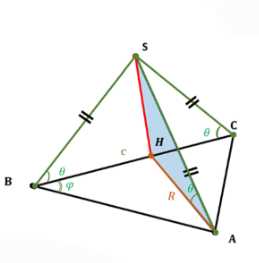
Найдите объём треугольной пирамиды \(SABC\), если: а) \(\angle CAB = 90°\), \(BC = c\), \(\angle ABC = \phi\) и каждое боковое ребро составляет с плоскостью основания угол \(\theta\); б) \(АВ = 12\) см, \(ВС = СА = 10\) см и двугранные углы при основании равны 45°; в) боковые рёбра попарно перпендикулярны и имеют длины \(a\), \(b\) и \(c\).

а) Объем пирамиды находится по формуле \(V = \frac{1}{3} S_{осн} \cdot h\). Высота пирамиды SH опускается в центр описанной окружности основания, который для прямоугольного треугольника лежит на середине гипотенузы. Радиус описанной окружности \(R = \frac{BC}{2} = \frac{c}{2}\).

Высота пирамиды \(h = SH = R \tan(\theta) = \frac{c}{2} \tan(\theta)\). Площадь основания \(S_{осн} = S_{\triangle ABC} = \frac{1}{2} AB \cdot AC\). В прямоугольном треугольнике ABC, \(AB = BC \cos(\phi) = c \cos(\phi)\) и \(AC = BC \sin(\phi) = c \sin(\phi)\). \(S_{осн} = \frac{1}{2} c \cos(\phi) c \sin(\phi) = \frac{1}{2} c^2 \sin(\phi) \cos(\phi) = \frac{1}{4} c^2 \sin(2\phi)\). Объем \(V = \frac{1}{3} \cdot \frac{1}{4} c^2 \sin(2\phi) \cdot \frac{c}{2} \tan(\theta) = \frac{c^3 \sin(2\phi) \tan(\theta)}{24}\). Ответ: \(V_{пирамиды} = \frac{\tan(\theta) \sin(2\phi) c^3}{24}\).

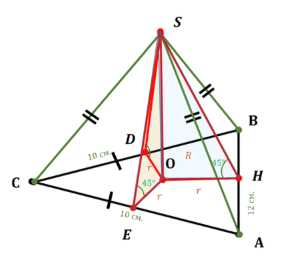
б) Объем пирамиды находится по формуле \(V = \frac{1}{3} S_{осн} \cdot h\). Поскольку двугранные углы при основании равны, высота пирамиды SO опускается в центр вписанной окружности основания.

Высота пирамиды равна радиусу вписанной окружности, умноженному на тангенс двугранного угла. Угол равен 45°, поэтому высота равна радиусу вписанной окружности \(h = r \tan(45°) = r\). Найдем площадь треугольника ABC по формуле Герона. Полупериметр \(p = \frac{10+10+12}{2} = 16\) см. Площадь \(S_{осн} = \sqrt{16(16-10)(16-10)(16-12)} = \sqrt{16 \cdot 6 \cdot 6 \cdot 4} = \sqrt{2304} = 48\) см². Радиус вписанной окружности \(r = \frac{S_{осн}}{p} = \frac{48}{16} = 3\) см. Высота пирамиды \(h = 3\) см. Объем \(V = \frac{1}{3} \cdot 48 \cdot 3 = 48\) см³. Ответ: \(V_{пирамиды} = 48\) см³.

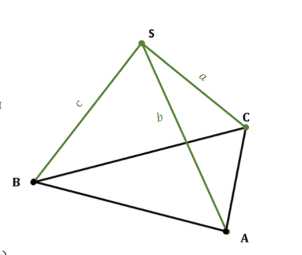
в) Объем пирамиды находится по формуле \(V = \frac{1}{3} S_{осн} \cdot h\). Если боковые ребра SA, SB, SC взаимно перпендикулярны, можно рассмотреть любую из граней, образованных двумя перпендикулярными ребрами, как основание, а третье ребро — как высоту.

Например, возьмем грань ACS как основание. Поскольку SA перпендикулярно SC, площадь \(\triangle ACS = \frac{1}{2} SA \cdot SC = \frac{1}{2} a \cdot c\). Ребро SB перпендикулярно как SA, так и SC, следовательно, SB перпендикулярно плоскости ACS. Таким образом, высота пирамиды с основанием ACS равна SB, то есть \(h = b\). Объем \(V = \frac{1}{3} S_{ACS} \cdot SB = \frac{1}{3} \cdot \frac{1}{2} ac \cdot b = \frac{abc}{6}\). Ответ: \(V_{пирамиды} = \frac{a \cdot b \cdot c}{6}\).

а) Объем пирамиды \(V\) находится по формуле \(V = \frac{1}{3} S_{осн} \cdot h\), где \(S_{осн}\) — площадь основания, а \(h\) — высота пирамиды. В данной пирамиде все боковые ребра составляют с плоскостью основания один и тот же угол \(\theta\).

Это означает, что основание высоты пирамиды совпадает с центром описанной окружности основания. Основанием является прямоугольный треугольник ABC с прямым углом при вершине A. Центр описанной окружности прямоугольного треугольника находится на середине гипотенузы. Гипотенузой является сторона BC, ее длина равна c. Пусть H — середина гипотенузы BC. Тогда H является основанием высоты пирамиды SH. Радиус описанной окружности \(R\) равен расстоянию от центра описанной окружности до любой вершины треугольника, то есть \(R = AH = BH = CH\). Для прямоугольного треугольника радиус описанной окружности равен половине гипотенузы, следовательно, \(R = \frac{BC}{2} = \frac{c}{2}\). Рассмотрим прямоугольный треугольник SHB. Угол между боковым ребром SB и плоскостью основания равен \(\angle SBH = \theta\). Высота пирамиды \(h = SH\). В прямоугольном треугольнике SHB тангенс угла \(\theta\) равен отношению противолежащего катета SH к прилежащему катету BH: \(\tan(\theta) = \frac{SH}{BH}\). Отсюда, высота пирамиды \(h = SH = BH \tan(\theta) = R \tan(\theta) = \frac{c}{2} \tan(\theta)\). Теперь найдем площадь основания \(S_{осн}\), которая является площадью прямоугольного треугольника ABC. Площадь прямоугольного треугольника равна половине произведения его катетов: \(S_{осн} = \frac{1}{2} AB \cdot AC\). В прямоугольном треугольнике ABC, используя тригонометрические соотношения для угла \(\phi\), имеем \(AB = BC \cos(\phi) = c \cos(\phi)\) и \(AC = BC \sin(\phi) = c \sin(\phi)\). Тогда площадь основания \(S_{осн} = \frac{1}{2} (c \cos(\phi)) (c \sin(\phi)) = \frac{1}{2} c^2 \cos(\phi) \sin(\phi)\). Используя формулу двойного угла для синуса \(\sin(2\phi) = 2 \sin(\phi) \cos(\phi)\), можем записать \(\cos(\phi) \sin(\phi) = \frac{1}{2} \sin(2\phi)\). Подставляем это в формулу площади основания: \(S_{осн} = \frac{1}{2} c^2 \left(\frac{1}{2} \sin(2\phi)\right) = \frac{1}{4} c^2 \sin(2\phi)\). Теперь подставим найденные значения площади основания и высоты в формулу объема пирамиды: \(V = \frac{1}{3} S_{осн} \cdot h = \frac{1}{3} \left(\frac{1}{4} c^2 \sin(2\phi)\right) \cdot \left(\frac{c}{2} \tan(\theta)\right)\). Умножаем дроби: \(V = \frac{1 \cdot c^2 \sin(2\phi) \cdot c \tan(\theta)}{3 \cdot 4 \cdot 2} = \frac{c^3 \sin(2\phi) \tan(\theta)}{24}\). Таким образом, объем пирамиды равен \(\frac{\tan(\theta) \sin(2\phi) c^3}{24}\).

б) Объем пирамиды \(V\) находится по формуле \(V = \frac{1}{3} S_{осн} \cdot h\). В данной пирамиде все двугранные углы при основании равны 45°. Это означает, что основание высоты пирамиды совпадает с центром вписанной окружности основания. Пусть O — центр вписанной окружности треугольника ABC, и SO — высота пирамиды.

Высота пирамиды \(h\) связана с радиусом вписанной окружности \(r\) и двугранным углом \(\alpha\) соотношением \(h = r \tan(\alpha)\). В данном случае \(\alpha = 45°\), поэтому \(h = r \tan(45°) = r \cdot 1 = r\). Высота пирамиды равна радиусу вписанной окружности основания. Основанием является треугольник ABC со сторонами \(AB = 12\) см, \(BC = 10\) см, \(CA = 10\) см. Найдем площадь этого треугольника по формуле Герона. Сначала вычислим полупериметр \(p = \frac{AB + BC + CA}{2} = \frac{12 + 10 + 10}{2} = \frac{32}{2} = 16\) см. Теперь вычислим площадь \(S_{осн} = S_{\triangle ABC} = \sqrt{p(p-a)(p-b)(p-c)}\), где a, b, c — длины сторон треугольника. \(S_{осн} = \sqrt{16(16-12)(16-10)(16-10)} = \sqrt{16 \cdot 4 \cdot 6 \cdot 6} = \sqrt{16 \cdot 4 \cdot 36}\). Извлекаем квадратные корни: \(\sqrt{16} = 4\), \(\sqrt{4} = 2\), \(\sqrt{36} = 6\). \(S_{осн} = 4 \cdot 2 \cdot 6 = 48\) см². Теперь найдем радиус вписанной окружности \(r\) по формуле \(S_{осн} = p \cdot r\). Отсюда \(r = \frac{S_{осн}}{p} = \frac{48}{16} = 3\) см. Высота пирамиды \(h = r = 3\) см. Подставим площадь основания и высоту в формулу объема пирамиды: \(V = \frac{1}{3} S_{осн} \cdot h = \frac{1}{3} \cdot 48 \cdot 3\). Вычисляем объем: \(V = \frac{1}{3} \cdot 144 = 48\) см³. Таким образом, объем пирамиды равен 48 см³.

в) Объем пирамиды \(V\) находится по формуле \(V = \frac{1}{3} S_{осн} \cdot h\). В данной пирамиде боковые ребра попарно перпендикулярны и имеют длины \(a\), \(b\), \(c\). Пусть ребра SA, SB, SC взаимно перпендикулярны, и их длины равны SA = a, SB = b, SC = c. Это означает, что \(\angle ASB = \angle ASC = \angle BSC = 90°\).

В такой пирамиде удобно выбрать одну из граней, образованных двумя перпендикулярными ребрами, в качестве основания, а третье ребро — в качестве высоты. Например, выберем грань ACS в качестве основания. Поскольку ребра SA и SC перпендикулярны, треугольник ACS является прямоугольным с прямым углом при вершине S. Площадь основания \(S_{осн} = S_{\triangle ACS} = \frac{1}{2} SA \cdot SC = \frac{1}{2} a \cdot c\). Ребро SB перпендикулярно как ребру SA, так и ребру SC. Поскольку SA и SC лежат в плоскости основания ACS, ребро SB перпендикулярно плоскости ACS. Следовательно, SB является высотой пирамиды с основанием ACS. Высота пирамиды \(h = SB = b\). Теперь подставим площадь основания и высоту в формулу объема пирамиды: \(V = \frac{1}{3} S_{осн} \cdot h = \frac{1}{3} \left(\frac{1}{2} ac\right) \cdot b\). Умножаем дроби: \(V = \frac{1 \cdot ac \cdot b}{3 \cdot 2} = \frac{abc}{6}\). Мы могли бы также выбрать грань ASB в качестве основания и SC в качестве высоты, или грань BSC в качестве основания и SA в качестве высоты. В каждом случае объем будет одинаковым: \(V = \frac{1}{3} S_{\triangle ASB} \cdot SC = \frac{1}{3} \left(\frac{1}{2} ab\right) c = \frac{abc}{6}\) или \(V = \frac{1}{3} S_{\triangle BSC} \cdot SA = \frac{1}{3} \left(\frac{1}{2} bc\right) a = \frac{abc}{6}\). Таким образом, объем пирамиды равен \(\frac{a \cdot b \cdot c}{6}\).