ГДЗ по Геометрии 11 класс Номер 487 Атанасян — Подробные Ответы

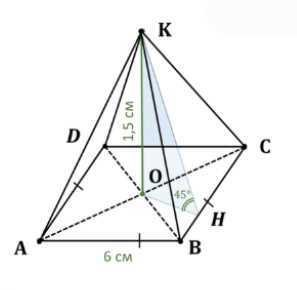
Основанием пирамиды является ромб со стороной 6 см. Каждый из двугранных углов при основании равен 45°. Найдите объём пирамиды, если её высота равна 1,5 см.

Вершина пирамиды проецируется в центр основания O. Так как двугранные углы при основании равны 45° и \(KO\) — высота, то треугольник \(KOH\) является прямоугольным равнобедренным, и \(OH = KO = 1.5\) см. Площадь треугольника \(BOC\) равна \(\frac{1}{2} \cdot OH \cdot BC = \frac{1}{2} \cdot 1.5 \cdot 6 = 4.5\) см². Объем пирамиды \(K-BOC\) равен \(\frac{1}{3} \cdot S_{BOC} \cdot KO = \frac{1}{3} \cdot 4.5 \cdot 1.5 = 2.25\) см³. Объем всей пирамиды \(ABCDK\) равен четырем объемам пирамиды \(K-BOC\), то есть \(4 \cdot 2.25 = 9\) см³.

Ответ: Объем пирамиды равен 9 см³.

Дано: пирамида \(ABCDK\) с основанием ромб \(ABCD\). Сторона ромба \(AB = 6\) см. Высота пирамиды \(KO = 1.5\) см, где O — точка на плоскости основания. Все двугранные углы при основании равны 45°. Найти: объем пирамиды \(V_{пирамиды}\).

Решение:
Поскольку все двугранные углы при основании равны, вершина пирамиды \(K\) проецируется в точку \(O\), которая является центром вписанной окружности ромба. В ромбе центр вписанной окружности совпадает с точкой пересечения диагоналей. Таким образом, \(O\) — точка пересечения диагоналей ромба \(ABCD\). \(KO\) является высотой пирамиды.

Рассмотрим двугранный угол при ребре основания \(BC\). Проведем из точки \(O\) перпендикуляр \(OH\) к стороне \(BC\). Тогда по теореме о трех перпендикулярах, \(KH\) перпендикулярен \(BC\). Угол \(\angle KHO\) является линейным углом двугранного угла при ребре \(BC\), и по условию он равен 45°.

Рассмотрим прямоугольный треугольник \(KOH\). Угол \(\angle KOH = 90°\) (так как \(KO\) — высота). Угол \(\angle KHO = 45°\). Сумма углов в треугольнике равна 180°, поэтому \(\angle OKH = 180° — 90° — 45° = 45°\). Так как углы при основании \(OH\) равны (\(\angle KHO = \angle OKH = 45°\)), треугольник \(KOH\) является равнобедренным с прямым углом, и \(OH = KO\).

По условию \(KO = 1.5\) см, следовательно, \(OH = 1.5\) см. Отрезок \(OH\) является высотой треугольника \(BOC\) из вершины \(O\) к стороне \(BC\). Также \(OH\) является радиусом вписанной окружности ромба.

Площадь треугольника \(BOC\) может быть найдена по формуле \(S_{BOC} = \frac{1}{2} \cdot BC \cdot OH\). Подставляя известные значения, получаем \(S_{BOC} = \frac{1}{2} \cdot 6 \cdot 1.5 = 3 \cdot 1.5 = 4.5\) см².

Объем пирамиды с вершиной \(K\) и основанием \(BOC\) (треугольная пирамида \(K-BOC\)) равен \(V_{K-BOC} = \frac{1}{3} \cdot S_{BOC} \cdot KO\). Подставляя значения, получаем \(V_{K-BOC} = \frac{1}{3} \cdot 4.5 \cdot 1.5 = 1.5 \cdot 1.5 = 2.25\) см³.

Поскольку диагонали ромба делят его на четыре равных треугольника (\(\triangle AOB\), \(\triangle BOC\), \(\triangle COD\), \(\triangle DOA\)), объем всей пирамиды \(ABCDK\) равен сумме объемов четырех пирамид с общей вершиной \(K\) и основаниями, равными этим треугольникам. В силу симметрии, объемы этих четырех пирамид равны. Таким образом, объем пирамиды \(ABCDK\) равен четырем объемам пирамиды \(K-BOC\).

\(V_{пирамиды} = 4 \cdot V_{K-BOC}\). Подставляем значение \(V_{K-BOC}\): \(V_{пирамиды} = 4 \cdot 2.25 = 9\) см³.

Ответ: Объем пирамиды равен 9 см³.