ГДЗ по Геометрии 11 класс Номер 485 Атанасян — Подробные Ответы

Основанием пирамиды является прямоугольный треугольник с катетами \(a\) и \(b\). Каждое её боковое ребро наклонено к плоскости основания под углом \(\phi\). Найдите объём пирамиды

Объём пирамиды находится по формуле \(V = \frac{1}{3} \cdot S_{осн} \cdot h\). Основанием является прямоугольный треугольник \(ABC\), его площадь \(S_{осн} = S_{\triangle ABC} = \frac{1}{2} \cdot AB \cdot AC = \frac{1}{2}ab\). Так как боковые ребра наклонены к плоскости основания под одним углом, высота пирамиды \(DH\) опускается в центр описанной окружности основания. Для прямоугольного треугольника центр описанной окружности находится на середине гипотенузы, поэтому \(H\) — середина \(BC\). Радиус описанной окружности \(R_{\triangle ABC} = \frac{BC}{2}\). По теореме Пифагора в \(\triangle ABC\), \(BC = \sqrt{AB^2 + AC^2} = \sqrt{a^2 + b^2}\). Следовательно, \(BH = R_{\triangle ABC} = \frac{\sqrt{a^2 + b^2}}{2}\). В прямоугольном треугольнике \(DHB\), высота \(DH = BH \cdot tg(\phi) = \frac{\sqrt{a^2 + b^2}}{2} \cdot tg(\phi)\). Подставляем значения в формулу объёма: \(V_{пирамиды} = \frac{1}{3} \cdot \frac{1}{2}ab \cdot \frac{\sqrt{a^2 + b^2}}{2} \cdot tg(\phi) = \frac{ab \cdot tg(\phi) \cdot \sqrt{a^2 + b^2}}{12}\). Ответ: \(V_{пирамиды} = \frac{a \cdot b \cdot tg(\phi) \sqrt{a^2+b^2}}{12}\).

Объём пирамиды \(ABCD\) с основанием \(\triangle ABC\) и высотой \(h\) вычисляется по формуле \(V = \frac{1}{3} \cdot S_{осн} \cdot h\).

Первым шагом найдем площадь основания пирамиды. Основанием является прямоугольный треугольник \(ABC\) с прямым углом при вершине \(A\). Длины катетов даны: \(AB = a\) и \(AC = b\). Площадь прямоугольного треугольника равна половине произведения его катетов. Таким образом, площадь основания \(S_{осн} = S_{\triangle ABC} = \frac{1}{2} \cdot AB \cdot AC = \frac{1}{2}ab\).

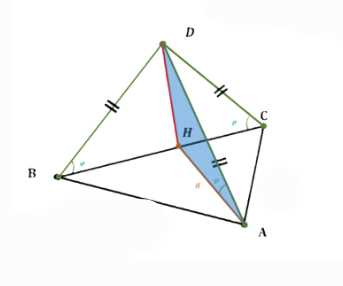
Далее определим положение основания высоты пирамиды. В условии сказано, что каждое боковое ребро наклонено к плоскости основания под одним и тем же углом \(\phi\). Это означает, что проекции боковых ребер на плоскость основания равны. Если \(H\) — основание высоты \(DH\) пирамиды, то \(HA\), \(HB\), \(HC\) — проекции боковых ребер \(DA\), \(DB\), \(DC\) на плоскость основания. Из равенства углов наклона следует, что треугольники \(DAH\), \(DBH\), \(DCH\) равны (по катету \(DH\) и острому углу \(\phi\)). Из равенства этих треугольников следует равенство их соответствующих сторон: \(HA = HB = HC\). Точка \(H\) равноудалена от всех вершин основания \(\triangle ABC\). По определению, такая точка является центром описанной окружности около \(\triangle ABC\).

Основание \(\triangle ABC\) является прямоугольным треугольником с прямым углом при вершине \(A\). Известно, что центр описанной окружности прямоугольного треугольника лежит на середине его гипотенузы. Гипотенузой в \(\triangle ABC\) является сторона \(BC\). Найдем длину гипотенузы \(BC\) по теореме Пифагора: \(BC^2 = AB^2 + AC^2\). Подставляя данные значения катетов, получаем \(BC^2 = a^2 + b^2\), откуда \(BC = \sqrt{a^2 + b^2}\).

Так как \(H\) — середина гипотенузы \(BC\), расстояние от \(H\) до любой вершины треугольника равно радиусу описанной окружности \(R_{\triangle ABC}\). Для прямоугольного треугольника радиус описанной окружности равен половине гипотенузы: \(R_{\triangle ABC} = \frac{BC}{2} = \frac{\sqrt{a^2 + b^2}}{2}\). Таким образом, \(HA = HB = HC = \frac{\sqrt{a^2 + b^2}}{2}\).

Теперь найдем высоту пирамиды \(h = DH\). Рассмотрим прямоугольный треугольник \(DHB\). Угол \(DBH\) равен \(\phi\) по условию (так как \(\angle DBH = \angle DAH = \angle DCH = \phi\)). В этом треугольнике \(BH\) является прилежащим катетом к углу \(\phi\), а \(DH\) — противолежащим катетом. Связь между катетами и углом дается тангенсом: \(tg(\phi) = \frac{DH}{BH}\). Отсюда выразим высоту \(DH\): \(DH = BH \cdot tg(\phi)\). Подставляя значение \(BH\), получаем \(h = DH = \frac{\sqrt{a^2 + b^2}}{2} \cdot tg(\phi)\).

Наконец, подставим найденные значения площади основания и высоты в формулу объёма пирамиды: \(V_{пирамиды} = \frac{1}{3} \cdot S_{осн} \cdot h = \frac{1}{3} \cdot \left(\frac{1}{2}ab\right) \cdot \left(\frac{\sqrt{a^2 + b^2}}{2} \cdot tg(\phi)\right)\).

Выполним умножение: \(V_{пирамиды} = \frac{1 \cdot ab \cdot \sqrt{a^2 + b^2} \cdot tg(\phi)}{3 \cdot 2 \cdot 2} = \frac{ab \cdot tg(\phi) \cdot \sqrt{a^2 + b^2}}{12}\).

Таким образом, объём пирамиды равен \(V_{пирамиды} = \frac{ab \cdot tg(\phi) \sqrt{a^2+b^2}}{12}\).