Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 484 Атанасян — Подробные Ответы
Основание пирамиды — равнобедренный треугольник АВС, в котором \(АВ = ВС = 13\) см, \(АС = 10\) см. Каждое боковое ребро пирамиды образует с её высотой угол в 30°. Вычислите объём пирамиды.
Основание пирамиды — равнобедренный треугольник \(АВС\) с боковыми сторонами \(АВ = ВС = 13\) см и основанием \(АС = 10\) см. Высота пирамиды \(DO\) перпендикулярна плоскости основания. Каждое боковое ребро образует с высотой угол в 30°, то есть \(\angle ODA = \angle ODB = \angle ODC = 30^\circ\). Из равенства этих углов следует равенство прямоугольных треугольников \(\triangle ODA, \triangle ODB, \triangle ODC\) по катету (\(DO\)) и острому углу. Отсюда следует равенство боковых ребер (\(AD = BD = CD\)) и равенство проекций боковых ребер на плоскость основания (\(OA = OB = OC\)). Это означает, что точка \(O\) является центром описанной окружности около треугольника \(АВС\), и \(OA = OB = OC = R_{АВС}\), где \(R_{АВС}\) — радиус описанной окружности.
Объем пирамиды вычисляется по формуле \(V = \frac{1}{3} S_{осн} \cdot h\), где \(S_{осн}\) — площадь основания, \(h\) — высота пирамиды. В данном случае \(S_{осн} = S_{АВС}\) и \(h = DO\).
Для нахождения площади треугольника \(АВС\) используем формулу Герона. Полупериметр \(p = \frac{AB + BC + AC}{2} = \frac{13 + 13 + 10}{2} = \frac{36}{2} = 18\) см.
Площадь \(S_{АВС} = \sqrt{p(p-a)(p-b)(p-c)} = \sqrt{18(18-13)(18-13)(18-10)} =\)
\(\sqrt{18 \cdot 5 \cdot 5 \cdot 8} = \sqrt{3600} = 60\) см².
Радиус описанной окружности для треугольника \(АВС\) можно найти по формуле \(R_{АВС} = \frac{abc}{4S_{АВС}}\), но удобнее использовать свойство равнобедренного треугольника. Высота \(ВН\) к основанию \(АС\) является также медианой, поэтому \(АН = НС = \frac{1}{2} АС = \frac{1}{2} \cdot 10 = 5\) см. В прямоугольном треугольнике \(АВН\) по теореме Пифагора \(ВН = \sqrt{АВ^2 — АН^2} = \sqrt{13^2 — 5^2} = \sqrt{169 — 25} = \sqrt{144} = 12\) см.
Радиус описанной окружности \(R_{АВС}\) для равнобедренного треугольника можно найти как \(R_{АВС} = \frac{a^2}{2h_a}\), где \(a\) — боковая сторона, \(h_a\) — высота к основанию. \(R_{АВС} = \frac{AB^2}{2 \cdot BH} = \frac{13^2}{2 \cdot 12} = \frac{169}{24}\) см.
В прямоугольном треугольнике \(ODA\), \(\angle ODA = 30^\circ\), \(OA = R_{АВС}\). Высота пирамиды \(DO\) связана с \(OA\) и углом \(\angle ODA\) соотношением \(\tan(\angle ODA) = \frac{OA}{DO}\), откуда \(DO = \frac{OA}{\tan(\angle ODA)} = \frac{R_{АВС}}{\tan(30^\circ)} = R_{АВС} \cdot \cot(30^\circ) = \frac{169}{24} \cdot \sqrt{3}\) см.
Теперь вычислим объем пирамиды: \(V = \frac{1}{3} S_{АВС} \cdot DO = \frac{1}{3} \cdot 60 \cdot \frac{169}{24} \cdot \sqrt{3} = 20 \cdot \frac{169}{24} \cdot \sqrt{3} = \frac{5 \cdot 169}{6} \cdot \sqrt{3} = \frac{845\sqrt{3}}{6}\) см³.
Ответ: Объем пирамиды равен \(\frac{845\sqrt{3}}{6}\) см³.
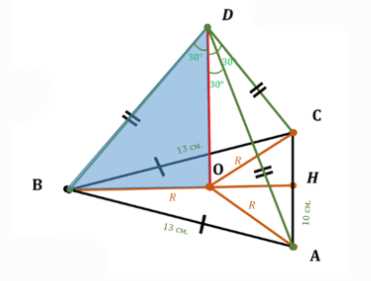
Дано: пирамида \(ABCD\), \(DO\) — высота, основание — треугольник \(ABC\), \(AB = BC = 13\) см, \(AC = 10\) см, \(\angle ODA = \angle ODB = \angle ODC = 30^\circ\). Найти: объем пирамиды \(V_{пирамиды}\).
Объем пирамиды находится по формуле \(V = \frac{1}{3} S_{осн} \cdot h\), где \(S_{осн}\) — площадь основания, а \(h\) — высота пирамиды. В данном случае \(S_{осн} = S_{АВС}\) и \(h = DO\).
Так как боковые ребра пирамиды образуют равные углы с высотой (\(\angle ODA = \angle ODB = \angle ODC = 30^\circ\)), а \(DO\) является общим катетом для прямоугольных треугольников \(\triangle ODA, \triangle ODB, \triangle ODC\), то эти треугольники равны по катету и острому углу. Из равенства треугольников следует равенство их гипотенуз (\(AD = BD = CD\)) и других катетов (\(OA = OB = OC\)). Равенство \(OA = OB = OC\) означает, что точка \(O\) является центром описанной окружности около треугольника \(АВС\), а \(OA = OB = OC = R_{АВС}\) — радиус этой описанной окружности.
Найдем площадь основания \(S_{АВС}\). Треугольник \(АВС\) — равнобедренный с боковыми сторонами \(AB = BC = 13\) см и основанием \(AC = 10\) см. Можно использовать формулу Герона для площади треугольника. Полупериметр \(p = \frac{AB + BC + AC}{2} = \frac{13 + 13 + 10}{2} = \frac{36}{2} = 18\) см.
Площадь треугольника \(АВС\) равна \(S_{АВС} = \sqrt{p(p-AB)(p-BC)(p-AC)} = \sqrt{18(18-13)(18-13)}\)
\(\sqrt{(18-10)} = \sqrt{18 \cdot 5 \cdot 5 \cdot 8} = \sqrt{(9 \cdot 2) \cdot 25 \cdot (4 \cdot 2)} = \sqrt{9 \cdot 25 \cdot 8 \cdot 2} =\)
\( \sqrt{9 \cdot 25 \cdot 16} = 3 \cdot 5 \cdot 4 = 60\) см².
Теперь найдем радиус описанной окружности \(R_{АВС}\). Для равнобедренного треугольника \(АВС\), высота \(ВН\), проведенная к основанию \(АС\), является также медианой. Следовательно, \(АН = \frac{1}{2} АС = \frac{1}{2} \cdot 10 = 5\) см. В прямоугольном треугольнике \(АВН\) по теореме Пифагора найдем высоту \(ВН\): \(ВН = \sqrt{AB^2 — AH^2} = \sqrt{13^2 — 5^2} = \sqrt{169 — 25} = \sqrt{144} = 12\) см.
Радиус описанной окружности для треугольника \(АВС\) можно найти по формуле \(R_{АВС} = \frac{abc}{4S_{АВС}}\) или, используя свойства равнобедренного треугольника, через синус угла. В прямоугольном треугольнике \(АВН\), \(\sin(\angle CAB) = \frac{BH}{AB} = \frac{12}{13}\). Радиус описанной окружности \(R_{АВС} = \frac{BC}{2 \cdot \sin(\angle CAB)} = \frac{13}{2 \cdot \frac{12}{13}} = \frac{13 \cdot 13}{2 \cdot 12} = \frac{169}{24}\) см.
Теперь найдем высоту пирамиды \(DO\). В прямоугольном треугольнике \(ODA\), \(\angle ODA = 30^\circ\) и \(OA = R_{АВС} = \frac{169}{24}\) см. Используем тригонометрическое соотношение: \(\tan(\angle ODA) = \frac{OA}{DO}\). Отсюда \(DO = \frac{OA}{\tan(\angle ODA)} = OA \cdot \cot(\angle ODA) = \frac{169}{24} \cdot \cot(30^\circ) = \frac{169}{24} \cdot \sqrt{3}\) см.
Наконец, вычислим объем пирамиды: \(V_{пирамиды} = \frac{1}{3} S_{АВС} \cdot DO = \frac{1}{3} \cdot 60 \cdot \frac{169}{24} \cdot \sqrt{3} = 20 \cdot \frac{169}{24} \cdot \sqrt{3} = \frac{20 \cdot 169 \cdot \sqrt{3}}{24}\). Сократим дробь на 4: \(\frac{5 \cdot 169 \cdot \sqrt{3}}{6} = \frac{845\sqrt{3}}{6}\) см³.
Ответ: Объем пирамиды равен \(\frac{845\sqrt{3}}{6}\) см³.
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.