
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 483 Атанасян — Подробные Ответы
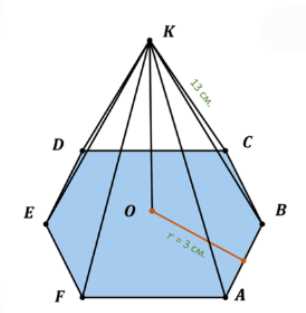
Найдите объём и площадь боковой поверхности правильной шестиугольной пирамиды, если её боковое ребро равно 13 см, а диаметр круга, вписанного в основание, равен 6 см.
Дано: правильная шестиугольная пирамида ABCDEFK, KO — высота, CK = 13 см, диаметр вписанного в основание круга d = 6 см. Найти: \(V_{пирамиды}\), \(S_{боковой\ пов.}\).
Решение:
Радиус вписанного круга в основание \(r = \frac{d}{2} = \frac{6}{2} = 3\) см.
Сторона правильного шестиугольника в основании \(AB = \frac{2r}{\sqrt{3}} = \frac{2 \cdot 3}{\sqrt{3}} = 2\sqrt{3}\) см.
Площадь основания \(S_{основания} = \frac{1}{2} \cdot P_{основания} \cdot r = \frac{1}{2} \cdot (6 \cdot AB) \cdot r = \frac{1}{2} \cdot (6 \cdot 2\sqrt{3}) \cdot 3 = 18\sqrt{3}\) см².
Радиус описанного круга вокруг основания \(R = AB = 2\sqrt{3}\) см.
Высота пирамиды \(h = KO = \sqrt{CK^2 — AO^2}\), где AO = R. \(h = \sqrt{13^2 — (2\sqrt{3})^2} = \sqrt{169 — 12} = \sqrt{157}\) см.
Объём пирамиды \(V_{пирамиды} = \frac{1}{3} \cdot S_{основания} \cdot h = \frac{1}{3} \cdot 18\sqrt{3} \cdot \sqrt{157} = 6\sqrt{3 \cdot 157} = 6\sqrt{471}\) см³.
Площадь боковой поверхности равна сумме площадей шести боковых граней. Найдем площадь одной боковой грани \(\triangle ABK\) по формуле Герона. Стороны треугольника: AB = \(2\sqrt{3}\) см, AK = BK = 13 см. Полупериметр \(p = \frac{2\sqrt{3} + 13 + 13}{2} = 13 + \sqrt{3}\) см.
Площадь \(\triangle ABK = \sqrt{p(p-a)(p-b)(p-c)} = \sqrt{(13+\sqrt{3})}\)
\(\sqrt{(13+\sqrt{3}-2\sqrt{3})(13+\sqrt{3}-13)(13+\sqrt{3}-13)} = \sqrt{(13+\sqrt{3})}\)
\(\sqrt{(13-\sqrt{3})(\sqrt{3})(\sqrt{3})} = \sqrt{(169-3) \cdot 3} = \sqrt{166 \cdot 3} = \sqrt{498}\) см².
Площадь боковой поверхности \(S_{боковой\ пов.} = 6 \cdot S_{\triangle ABK} = 6\sqrt{498}\) см².
Ответ: \(V_{пирамиды} = 6\sqrt{471}\) см³, \(S_{боковой\ пов.} = 6\sqrt{498}\) см².
Дано: правильная шестиугольная пирамида ABCDEFK, KO — высота пирамиды, CK = 13 см — длина бокового ребра, диаметр круга, вписанного в основание d = 6 см.
Найти: объём пирамиды \(V_{пирамиды}\) и площадь боковой поверхности \(S_{боковой\ пов.}\).
Решение:
Основанием правильной шестиугольной пирамиды является правильный шестиугольник ABCDEF. Высота пирамиды KO проецируется в центр основания O, который также является центром вписанной и описанной окружностей.
Радиус круга, вписанного в основание \(r_{ABCDEF}\), равен половине диаметра: \(r_{ABCDEF} = \frac{d}{2} = \frac{6}{2} = 3\) см.
Для правильного шестиугольника сторона \(AB\) связана с радиусом вписанного круга \(r_{ABCDEF}\) соотношением \(r_{ABCDEF} = \frac{AB\sqrt{3}}{2}\). Отсюда выразим сторону основания \(AB\): \(AB = \frac{2 \cdot r_{ABCDEF}}{\sqrt{3}} = \frac{2 \cdot 3}{\sqrt{3}} = \frac{6}{\sqrt{3}} = \frac{6\sqrt{3}}{3} = 2\sqrt{3}\) см.
Площадь основания \(S_{основания}\) правильного шестиугольника может быть найдена как половина произведения его периметра на радиус вписанной окружности: \(S_{основания} = \frac{1}{2} \cdot P_{ABCDEF} \cdot r_{ABCDEF}\). Периметр основания \(P_{ABCDEF}\) равен шести сторонам: \(P_{ABCDEF} = 6 \cdot AB = 6 \cdot 2\sqrt{3} = 12\sqrt{3}\) см.
Тогда площадь основания \(S_{основания} = \frac{1}{2} \cdot 12\sqrt{3} \cdot 3 = 18\sqrt{3}\) см².
Радиус описанного круга вокруг правильного шестиугольника \(R_{ABCDEF}\) равен его стороне: \(R_{ABCDEF} = AB = 2\sqrt{3}\) см. Точка A лежит на описанной окружности, поэтому расстояние от центра O до вершины A равно радиусу описанной окружности: \(AO = R_{ABCDEF} = 2\sqrt{3}\) см.
Рассмотрим прямоугольный треугольник \(\triangle KAO\), где KO — высота пирамиды, AO — радиус описанного круга основания, KA — боковое ребро (равное CK = 13 см). По теореме Пифагора найдем высоту \(KO\): \(KO^2 + AO^2 = KA^2\), следовательно, \(KO = \sqrt{KA^2 — AO^2} = \sqrt{13^2 — (2\sqrt{3})^2} = \sqrt{169 — (4 \cdot 3)} = \sqrt{169 — 12} =\)
\( \sqrt{157}\) см.
Объём пирамиды \(V_{пирамиды}\) вычисляется по формуле \(V = \frac{1}{3} \cdot S_{основания} \cdot h\), где \(h = KO\).
\(V_{пирамиды} = \frac{1}{3} \cdot 18\sqrt{3} \cdot \sqrt{157} = 6\sqrt{3} \cdot \sqrt{157} = 6\sqrt{3 \cdot 157} = 6\sqrt{471}\) см³.
Площадь боковой поверхности \(S_{боковой\ пов.}\) правильной пирамиды равна сумме площадей всех боковых граней. В правильной шестиугольной пирамиде все 6 боковых граней являются равными равнобедренными треугольниками. Рассмотрим грань \(\triangle ABK\). Стороны этого треугольника: \(AB = 2\sqrt{3}\) см, \(AK = BK = 13\) см.
Для нахождения площади \(\triangle ABK\) воспользуемся формулой Герона. Полупериметр \(p = \frac{AB + AK + BK}{2} = \frac{2\sqrt{3} + 13 + 13}{2} = \frac{2\sqrt{3} + 26}{2} = \sqrt{3} + 13\) см.
Площадь \(\triangle ABK = \sqrt{p(p-AB)(p-AK)(p-BK)} = \sqrt{(13+\sqrt{3})}\)
\(\sqrt{(13+\sqrt{3}-2\sqrt{3})(13+\sqrt{3}-13)(13+\sqrt{3}-13)} = \sqrt{(13+\sqrt{3})}\)
\(\sqrt{(13-\sqrt{3})(\sqrt{3})(\sqrt{3})}\).
Используем формулу разности квадратов \((a+b)(a-b) = a^2 — b^2\): \((13+\sqrt{3})(13-\sqrt{3}) = 13^2 — (\sqrt{3})^2 = 169 — 3 = 166\).
Тогда площадь \(\triangle ABK = \sqrt{166 \cdot (\sqrt{3})^2} = \sqrt{166 \cdot 3} = \sqrt{498}\) см².
Площадь боковой поверхности \(S_{боковой\ пов.} = 6 \cdot S_{\triangle ABK} = 6 \cdot \sqrt{498}\) см².
Ответ: \(V_{пирамиды} = 6\sqrt{471}\) см³, \(S_{боковой\ пов.} = 6\sqrt{498}\) см².
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!