Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 482 Атанасян — Подробные Ответы
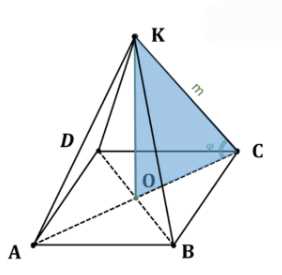
Боковое ребро правильной четырёхугольной пирамиды равно \(m\) и составляет с плоскостью основания угол \(\phi\). Найдите объём пирамиды.
Решение: Объем пирамиды находится по формуле \(V = \frac{1}{3} S_{\text{основания}} \cdot h\).
В прямоугольном треугольнике ДКОС, где КО — высота пирамиды, ОС является проекцией бокового ребра КС на плоскость основания.
Дано \(KC = m\) и \(\angle OCK = \phi\).
Высота пирамиды \(h = KO = KC \cdot \sin(\phi) = m \sin(\phi)\).
Отрезок \(OC = KC \cdot \cos(\phi) = m \cos(\phi)\).
Поскольку основание ABCD — квадрат, AC является его диагональю, и \(AC = 2 \cdot OC = 2 m \cos(\phi)\).
Площадь основания \(S_{\text{основания}} = S_{\text{ABCD}} = \frac{AC^2}{2} = \frac{(2 m \cos(\phi))^2}{2} = \frac{4 m^2 \cos^2(\phi)}{2} = 2 m^2 \cos^2(\phi)\).
Подставляем значения площади основания и высоты в формулу объема пирамиды:
\(V_{\text{пирамиды}} = \frac{1}{3} \cdot (2 m^2 \cos^2(\phi)) \cdot (m \sin(\phi)) = \frac{2 m^3 \cos^2(\phi) \sin(\phi)}{3}\).
Используя формулу двойного угла для синуса \(\sin(2\phi) = 2 \sin(\phi) \cos(\phi)\), преобразуем выражение:
\(V_{\text{пирамиды}} = \frac{m^3}{3} \cdot (2 \sin(\phi) \cos(\phi)) \cdot \cos(\phi) = \frac{m^3 \sin(2\phi) \cos(\phi)}{3}\).
Ответ: \(V_{\text{пирамиды}} = \frac{m^3 \sin(2\phi) \cos(\phi)}{3}\).
Решение:
Объем пирамиды \(V\) определяется формулой \(V = \frac{1}{3} S_{\text{основания}} \cdot h\), где \(S_{\text{основания}}\) — площадь основания, а \(h\) — высота пирамиды.
В данной правильной четырехугольной пирамиде ABCDK основанием является квадрат ABCD, а высота КО опущена в центр основания О. Боковое ребро СК равно \(m\), и угол между боковым ребром СК и плоскостью основания (углом LOCK) равен \(\phi\). В данном случае, угол между боковым ребром СК и его проекцией ОС на плоскость основания ABCD — это угол \(\angle OCK = \phi\).
Рассмотрим прямоугольный треугольник KOC. В этом треугольнике:
— Гипотенуза KC = \(m\).
— Катет KO является высотой пирамиды \(h\).
— Катет OC является половиной диагонали основания AC, так как О — центр квадрата.
Используя тригонометрические соотношения в прямоугольном треугольнике KOC:
Высота пирамиды \(h = KO = KC \cdot \sin(\angle OCK) = m \sin(\phi)\).
Длина отрезка \(OC = KC \cdot \cos(\angle OCK) = m \cos(\phi)\).
Основание пирамиды — квадрат ABCD. Точка О является центром квадрата, поэтому ОС — это половина диагонали AC.
Длина диагонали основания \(AC = 2 \cdot OC = 2 \cdot (m \cos(\phi)) = 2m \cos(\phi)\).
Площадь квадрата можно найти по формуле \(S = a^2\), где \(a\) — сторона квадрата, или через диагональ \(d\) по формуле \(S = \frac{d^2}{2}\). Используем формулу через диагональ AC:
Площадь основания \(S_{\text{основания}} = S_{\text{ABCD}} = \frac{AC^2}{2} = \frac{(2m \cos(\phi))^2}{2} = \frac{4m^2 \cos^2(\phi)}{2} = 2m^2 \cos^2(\phi)\).
Теперь подставим найденные значения площади основания \(S_{\text{основания}}\) и высоты \(h\) в формулу объема пирамиды:
\(V_{\text{пирамиды}} = \frac{1}{3} \cdot S_{\text{основания}} \cdot h = \frac{1}{3} \cdot (2m^2 \cos^2(\phi)) \cdot (m \sin(\phi))\).
\(V_{\text{пирамиды}} = \frac{2 m^2 \cos^2(\phi) \cdot m \sin(\phi)}{3} = \frac{2 m^3 \cos^2(\phi) \sin(\phi)}{3}\).
Для того чтобы привести ответ к виду, представленному в примере, воспользуемся формулой синуса двойного угла: \(\sin(2\phi) = 2 \sin(\phi) \cos(\phi)\).
Перегруппируем множители в выражении для объема:
\(V_{\text{пирамиды}} = \frac{m^3}{3} \cdot (2 \cos(\phi) \sin(\phi)) \cdot \cos(\phi)\).
Заменяем \(2 \sin(\phi) \cos(\phi)\) на \(\sin(2\phi)\):
\(V_{\text{пирамиды}} = \frac{m^3}{3} \cdot \sin(2\phi) \cdot \cos(\phi) = \frac{m^3 \sin(2\phi) \cos(\phi)}{3}\).
Таким образом, объем пирамиды равен \(\frac{m^3 \sin(2\phi) \cos(\phi)}{3}\).
Ответ: \(V_{\text{пирамиды}} = \frac{m^3 \sin(2\phi) \cos(\phi)}{3}\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.