
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 481 Атанасян — Подробные Ответы
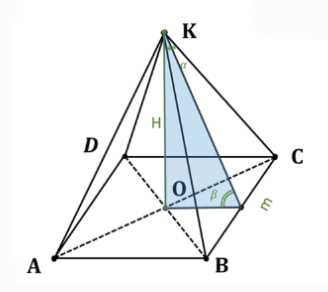
Найдите объём правильной четырёхугольной пирамиды, если: а) её высота равна \(Н\), а двугранный угол при основании равен \(\beta\); б) сторона основания равна \(m\), а плоский угол при вершине равен \(\alpha\).
Решение:
а) Поскольку \(ABCD\) — квадрат, то \(S_{ABCD} = AB^2 = (2 \cdot \frac{H}{\text{tg}(\beta)})^2\). Объем пирамиды равен \(V_{\text{пирамиды}} = \frac{1}{3} \cdot S_{\text{основания}} \cdot H = \frac{1}{3} \cdot (2 \cdot \frac{H}{\text{tg}(\beta)})^2 \cdot H = \frac{4 H^3}{3 \text{tg}^2(\beta)}\).
б) Поскольку \(\triangle BKC\) — равнобедренный, высота, проведенная к основанию, является медианой, то есть \(\frac{1}{2} BC = KC \cdot \sin(\frac{\alpha}{2})\), откуда \(KC = \frac{m}{2 \sin(\frac{\alpha}{2})}\). Так как \(ABCD\) — квадрат, \(S_{ABCD} = AB^2 = m^2\), а \(CO = \frac{m}{\sqrt{2}}\). По теореме Пифагора из прямоугольного \(\triangle KCO\), \(KO = \sqrt{KC^2 — CO^2} = \sqrt{(\frac{m}{2 \sin(\frac{\alpha}{2})})^2 — (\frac{m}{\sqrt{2}})^2} = \sqrt{\frac{m^2}{4 \sin^2(\frac{\alpha}{2})} — \frac{m^2}{2}} = \)
\(= \sqrt{\frac{m^2 — 2m^2 \sin^2(\frac{\alpha}{2})}{4 \sin^2(\frac{\alpha}{2})}} = m \sqrt{\frac{1 — 2 \sin^2(\frac{\alpha}{2})}{4 \sin^2(\frac{\alpha}{2})}} = m \frac{\sqrt{\cos(\alpha)}}{2 \sin(\frac{\alpha}{2})}\). Объем пирамиды равен \(V_{\text{пирамиды}} = \frac{1}{3} \cdot S_{\text{основания}} \cdot KO = \frac{1}{3} \cdot m^2 \cdot m \frac{\sqrt{\cos(\alpha)}}{2 \sin(\frac{\alpha}{2})} = \frac{m^3 \sqrt{\cos(\alpha)}}{6 \sin(\frac{\alpha}{2})}\).
Ответ:
а) \(V_{\text{пирамиды}} = \frac{4 H^3}{3 \text{tg}^2(\beta)}\)
б) \(V_{\text{пирамиды}} = \frac{m^3 \sqrt{\cos(\alpha)}}{6 \sin(\frac{\alpha}{2})}\)
Для нахождения объема правильной четырехугольной пирамиды воспользуемся формулой объема пирамиды \(V = \frac{1}{3} \cdot S_{\text{основания}} \cdot h\), где \(S_{\text{основания}}\) — площадь основания, а \(h\) — высота пирамиды. В данной правильной четырехугольной пирамиде \(ABCDK\) основанием является квадрат \(ABCD\), а высота — отрезок \(KO\), где \(O\) — центр квадрата \(ABCD\).
а) Дано: высота пирамиды \(KO = H\), двугранный угол при основании \(\angle DBCK = \beta\).
Поскольку \(ABCD\) — квадрат, его площадь \(S_{ABCD} = AB^2\). Для нахождения стороны квадрата \(AB\) рассмотрим двугранный угол при основании. Двугранный угол \(\angle DBCK\) измеряется линейным углом в сечении, перпендикулярном ребру \(BC\). Проведем апофему \(KM\) боковой грани \(BCK\), где \(M\) — середина \(BC\). Тогда \(KM \perp BC\). Поскольку \(O\) — центр квадрата, \(OM \perp BC\). Угол между плоскостью основания \(ABCD\) и плоскостью боковой грани \(BCK\) — это угол между перпендикулярами к общей линии \(BC\), то есть \(\angle KMO = \beta\).
В прямоугольном треугольнике \(KMO\) имеем \(KO = H\) и \(\angle KMO = \beta\). Используем определение тангенса: \(\text{tg}(\beta) = \frac{KO}{OM}\). Отсюда \(OM = \frac{KO}{\text{tg}(\beta)} = \frac{H}{\text{tg}(\beta)}\).
Так как \(O\) — центр квадрата \(ABCD\) и \(M\) — середина стороны \(BC\), длина отрезка \(OM\) равна половине длины стороны квадрата \(AB\). Следовательно, \(AB = 2 \cdot OM = 2 \cdot \frac{H}{\text{tg}(\beta)}\).
Площадь основания \(S_{ABCD} = AB^2 = (2 \cdot \frac{H}{\text{tg}(\beta)})^2 = \frac{4 H^2}{\text{tg}^2(\beta)}\).
Теперь найдем объем пирамиды: \(V_{\text{пирамиды}} = \frac{1}{3} \cdot S_{ABCD} \cdot KO = \frac{1}{3} \cdot \frac{4 H^2}{\text{tg}^2(\beta)} \cdot H = \frac{4 H^3}{3 \text{tg}^2(\beta)}\).
б) Дано: сторона основания \(BC = m\), плоский угол при вершине \(\angle BKC = \alpha\).
Поскольку \(ABCD\) — квадрат со стороной \(m\), площадь основания \(S_{ABCD} = m^2\).
Для нахождения высоты пирамиды \(KO\) рассмотрим боковую грань \(\triangle BKC\). Эта грань является равнобедренным треугольником, так как боковые ребра правильной пирамиды равны (\(BK = CK\)). Угол при вершине \(\angle BKC = \alpha\), основание \(BC = m\). Проведем высоту \(KM\) к основанию \(BC\), где \(M\) — середина \(BC\). В равнобедренном треугольнике высота \(KM\) также является медианой и биссектрисой угла \(\angle BKC\).
В прямоугольном треугольнике \(KMC\) имеем \(\angle MKC = \frac{\alpha}{2}\) и \(MC = \frac{BC}{2} = \frac{m}{2}\). Используем определение синуса: \(\sin(\frac{\alpha}{2}) = \frac{MC}{KC}\). Отсюда найдем длину бокового ребра \(KC = \frac{MC}{\sin(\frac{\alpha}{2})} = \frac{m/2}{\sin(\frac{\alpha}{2})} = \frac{m}{2 \sin(\frac{\alpha}{2})}\).
Теперь рассмотрим прямоугольный треугольник \(KOC\). В нем \(KO\) — высота пирамиды, \(OC\) — половина диагонали квадрата основания, а \(KC\) — боковое ребро.
Диагональ квадрата \(ABCD\) со стороной \(m\) равна \(AC = \sqrt{AB^2 + BC^2} = \sqrt{m^2 + m^2} = m\sqrt{2}\).
Отрезок \(OC\) равен половине диагонали \(AC\), то есть \(OC = \frac{AC}{2} = \frac{m\sqrt{2}}{2} = \frac{m}{\sqrt{2}}\).
По теореме Пифагора в прямоугольном треугольнике \(KOC\): \(KO^2 + OC^2 = KC^2\).
Выразим \(KO^2\): \(KO^2 = KC^2 — OC^2 = (\frac{m}{2 \sin(\frac{\alpha}{2})})^2 — (\frac{m}{\sqrt{2}})^2 = \frac{m^2}{4 \sin^2(\frac{\alpha}{2})} — \frac{m^2}{2}\).
Приведем к общему знаменателю: \(KO^2 = \frac{m^2 — 2m^2 \sin^2(\frac{\alpha}{2})}{4 \sin^2(\frac{\alpha}{2})} = \frac{m^2(1 — 2 \sin^2(\frac{\alpha}{2}))}{4 \sin^2(\frac{\alpha}{2})}\).
Используя тригонометрическую формулу \(1 — 2 \sin^2(x) = \cos(2x)\), получим \(1 — 2 \sin^2(\frac{\alpha}{2}) = \cos(2 \cdot \frac{\alpha}{2}) = \cos(\alpha)\).
Следовательно, \(KO^2 = \frac{m^2 \cos(\alpha)}{4 \sin^2(\frac{\alpha}{2})}\).
Высота пирамиды \(KO = \sqrt{\frac{m^2 \cos(\alpha)}{4 \sin^2(\frac{\alpha}{2})}} = \frac{\sqrt{m^2 \cos(\alpha)}}{\sqrt{4 \sin^2(\frac{\alpha}{2})}} = \frac{m \sqrt{\cos(\alpha)}}{2 |\sin(\frac{\alpha}{2})|}\). Поскольку \(\alpha\) — плоский угол при вершине правильной пирамиды, \(0 < \alpha < 180^\circ\), и для четырехугольной пирамиды сумма плоских углов при вершине меньше \(360^\circ\), то есть \(4\alpha < 360^\circ\), откуда \(\alpha < 90^\circ\). Следовательно, \(\frac{\alpha}{2} < 45^\circ\), и \(\sin(\frac{\alpha}{2}) > 0\). Также \(\cos(\alpha) > 0\).
Таким образом, \(KO = \frac{m \sqrt{\cos(\alpha)}}{2 \sin(\frac{\alpha}{2})}\).
Теперь найдем объем пирамиды: \(V_{\text{пирамиды}} = \frac{1}{3} \cdot S_{ABCD} \cdot KO = \frac{1}{3} \cdot m^2 \cdot \frac{m \sqrt{\cos(\alpha)}}{2 \sin(\frac{\alpha}{2})} = \frac{m^3 \sqrt{\cos(\alpha)}}{6 \sin(\frac{\alpha}{2})}\).
Ответ:
а) \(V_{\text{пирамиды}} = \frac{4 H^3}{3 \text{tg}^2(\beta)}\)
б) \(V_{\text{пирамиды}} = \frac{m^3 \sqrt{\cos(\alpha)}}{6 \sin(\frac{\alpha}{2})}\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!