ГДЗ по Геометрии 11 класс Номер 480 Атанасян — Подробные Ответы

В правильной треугольной пирамиде плоский угол при вершине равен \(\phi\), а сторона основания равна \(a\). Найдите объём пирамиды.

Объём пирамиды находится по формуле \(V = \frac{1}{3} S_{осн} \cdot h\). Основание — равносторонний треугольник со стороной \(a\), его площадь \(S_{осн} = \frac{\sqrt{3}}{4} a^2\). В равнобедренном треугольнике \(ADB\) высота к основанию \(AB\) является медианой. Из прямоугольного треугольника имеем \(\frac{a}{2} = AD \sin(\frac{\phi}{2})\), откуда \(AD = \frac{a}{2 \sin(\frac{\phi}{2})}\). Центр основания \(O\) является центром описанной окружности для равностороннего треугольника \(ABC\), радиус \(AO = R = \frac{a}{\sqrt{3}}\). Высота пирамиды \(h = DO\) находится из прямоугольного треугольника \(ADO\) по теореме Пифагора: \(h = \sqrt{AD^2 — AO^2} = \sqrt{\left(\frac{a}{2 \sin(\frac{\phi}{2})}\right)^2 — \left(\frac{a}{\sqrt{3}}\right)^2} = \sqrt{\frac{a^2}{4 \sin^2(\frac{\phi}{2})} — \frac{a^2}{3}} =\)
\(= \sqrt{\frac{3a^2 — 4a^2 \sin^2(\frac{\phi}{2})}{12 \sin^2(\frac{\phi}{2})}} = a \sqrt{\frac{3 — 4 \sin^2(\frac{\phi}{2})}{12 \sin^2(\frac{\phi}{2})}}\). Подставляем \(S_{осн}\) и \(h\) в формулу объёма: \(V = \frac{1}{3} \cdot \frac{\sqrt{3}}{4} a^2 \cdot a \sqrt{\frac{3 — 4 \sin^2(\frac{\phi}{2})}{12 \sin^2(\frac{\phi}{2})}}\). Упрощаем выражение: \(V = \frac{\sqrt{3}}{12} a^3 \frac{\sqrt{3 — 4 \sin^2(\frac{\phi}{2})}}{\sqrt{12} \sin(\frac{\phi}{2})} = \frac{\sqrt{3} a^3 \sqrt{3 — 4 \sin^2(\frac{\phi}{2})}}{12 \cdot 2\sqrt{3} \sin(\frac{\phi}{2})} = \frac{a^3 \sqrt{3 — 4 \sin^2(\frac{\phi}{2})}}{24 \sin(\frac{\phi}{2})}\). Ответ: \(V_{пирамиды} = \frac{a^3 \sqrt{3 — 4 \sin^2(\frac{\phi}{2})}}{24 \sin(\frac{\phi}{2})}\).

Объём правильной пирамиды находится по формуле \(V = \frac{1}{3} S_{осн} \cdot h\), где \(S_{осн}\) — площадь основания, а \(h\) — высота пирамиды.

Основанием данной пирамиды является равносторонний треугольник \(ABC\) со стороной \(a\). Площадь равностороннего треугольника со стороной \(a\) вычисляется по формуле \(S_{осн} = \frac{\sqrt{3}}{4} a^2\).

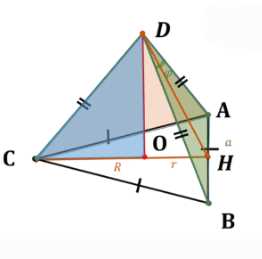
Рассмотрим боковую грань \(ADB\). Это равнобедренный треугольник, так как пирамида правильная, и боковые ребра равны. Угол при вершине \(D\) между боковыми ребрами \(AD\) и \(BD\) равен \(\phi\). Высота, проведенная из вершины \(D\) к основанию \(AB\), является медианой и биссектрисой. Обозначим середину \(AB\) как \(H\). В прямоугольном треугольнике \(ADH\) имеем \(\angle ADH = \frac{\phi}{2}\). По определению синуса в прямоугольном треугольнике \(AH = AD \sin(\angle ADH)\). Поскольку \(AH = \frac{1}{2} AB = \frac{a}{2}\), получаем \(\frac{a}{2} = AD \sin(\frac{\phi}{2})\). Отсюда выражаем длину бокового ребра \(AD = \frac{a}{2 \sin(\frac{\phi}{2})}\).

Высота правильной пирамиды опускается из вершины \(D\) в центр основания \(O\). Для равностороннего треугольника центр описанной окружности совпадает с центром тяжести и ортоцентром. Расстояние от вершины равностороннего треугольника до центра описанной окружности (радиус описанной окружности \(R\)) вычисляется по формуле \(R = \frac{a}{\sqrt{3}}\). Следовательно, \(AO = R = \frac{a}{\sqrt{3}}\).

Теперь рассмотрим прямоугольный треугольник \(ADO\). По теореме Пифагора квадрат высоты пирамиды \(DO^2\) равен разности квадратов бокового ребра \(AD^2\) и радиуса описанной окружности основания \(AO^2\). То есть \(h^2 = DO^2 = AD^2 — AO^2\). Подставляем найденные значения \(AD\) и \(AO\):
\(h^2 = \left(\frac{a}{2 \sin(\frac{\phi}{2})}\right)^2 — \left(\frac{a}{\sqrt{3}}\right)^2 = \frac{a^2}{4 \sin^2(\frac{\phi}{2})} — \frac{a^2}{3}\).
Приводим к общему знаменателю:
\(h^2 = \frac{3a^2 — 4a^2 \sin^2(\frac{\phi}{2})}{12 \sin^2(\frac{\phi}{2})} = \frac{a^2(3 — 4 \sin^2(\frac{\phi}{2}))}{12 \sin^2(\frac{\phi}{2})}\).
Извлекаем квадратный корень для нахождения высоты \(h\):
\(h = \sqrt{\frac{a^2(3 — 4 \sin^2(\frac{\phi}{2}))}{12 \sin^2(\frac{\phi}{2})}} = \frac{a \sqrt{3 — 4 \sin^2(\frac{\phi}{2})}}{\sqrt{12} \sin(\frac{\phi}{2})} = \frac{a \sqrt{3 — 4 \sin^2(\frac{\phi}{2})}}{2\sqrt{3} \sin(\frac{\phi}{2})}\).

Теперь подставляем значения площади основания \(S_{осн}\) и высоты \(h\) в формулу объёма пирамиды \(V = \frac{1}{3} S_{осн} \cdot h\):
\(V = \frac{1}{3} \cdot \frac{\sqrt{3}}{4} a^2 \cdot \frac{a \sqrt{3 — 4 \sin^2(\frac{\phi}{2})}}{2\sqrt{3} \sin(\frac{\phi}{2})}\).
Умножаем числители и знаменатели:
\(V = \frac{\sqrt{3} \cdot a^2 \cdot a \sqrt{3 — 4 \sin^2(\frac{\phi}{2})}}{3 \cdot 4 \cdot 2\sqrt{3} \sin(\frac{\phi}{2})} = \frac{\sqrt{3} a^3 \sqrt{3 — 4 \sin^2(\frac{\phi}{2})}}{24\sqrt{3} \sin(\frac{\phi}{2})}\).
Сокращаем \(\sqrt{3}\) в числителе и знаменателе:
\(V = \frac{a^3 \sqrt{3 — 4 \sin^2(\frac{\phi}{2})}}{24 \sin(\frac{\phi}{2})}\).

Таким образом, объём пирамиды равен \(\frac{a^3 \sqrt{3 — 4 \sin^2(\frac{\phi}{2})}}{24 \sin(\frac{\phi}{2})}\).