
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 478 Атанасян — Подробные Ответы
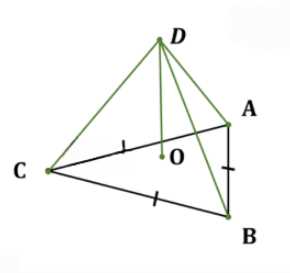
Найдите объём правильной треугольной пирамиды, высота которой равна 12 см, а сторона основания равна 13 см.
Решение:
Объем пирамиды находится по формуле \(V = \frac{1}{3} \cdot S_{основания} \cdot h\).
Основанием является правильный треугольник, площадь которого равна \(S_{основания} = \frac{a^2 \sqrt{3}}{4}\), где \(a\) — длина стороны основания.
Подставляем значение площади основания в формулу объема пирамиды: \(V = \frac{1}{3} \cdot \frac{a^2 \sqrt{3}}{4} \cdot h\).
Дано: \(a = 13\) см, \(h = 12\) см.
Подставляем значения: \(V = \frac{1}{3} \cdot \frac{13^2 \sqrt{3}}{4} \cdot 12 = \frac{1}{3} \cdot \frac{169 \sqrt{3}}{4} \cdot 12\).
Вычисляем: \(V = \frac{169 \sqrt{3} \cdot 12}{3 \cdot 4} = \frac{169 \sqrt{3} \cdot 12}{12} = 169 \sqrt{3}\) см³.
Ответ: \(V_{пирамиды} = 169 \sqrt{3}\) см³.
Решение задачи нахождения объема правильной треугольной пирамиды.
Сначала запишем формулу для нахождения объема любой пирамиды. Объем пирамиды \(V\) равен одной трети произведения площади ее основания \(S_{основания}\) на высоту \(h\). Математически это выражается так: \(V = \frac{1}{3} \cdot S_{основания} \cdot h\).
В данной задаче основанием пирамиды является треугольник ABC, у которого все стороны равны: AB = BC = CA = 13 см. Это означает, что основание является правильным (равносторонним) треугольником.
Далее необходимо найти площадь основания, то есть площадь правильного треугольника со стороной \(a = 13\) см. Площадь правильного треугольника со стороной \(a\) вычисляется по формуле \(S_{основания} = \frac{a^2 \sqrt{3}}{4}\).
Подставляем значение стороны \(a = 13\) см в формулу площади основания: \(S_{основания} = \frac{13^2 \sqrt{3}}{4} = \frac{169 \sqrt{3}}{4}\) см².
Теперь у нас есть площадь основания \(S_{основания} = \frac{169 \sqrt{3}}{4}\) см² и дана высота пирамиды \(h = 12\) см. Подставим эти значения в формулу объема пирамиды \(V = \frac{1}{3} \cdot S_{основания} \cdot h\).
Получаем: \(V = \frac{1}{3} \cdot \frac{169 \sqrt{3}}{4} \cdot 12\).
Выполним умножение. Сначала можно умножить \(\frac{1}{3}\) на \(12\), что даст \(4\). Тогда выражение примет вид: \(V = \frac{169 \sqrt{3}}{4} \cdot 4\).
Теперь умножаем \(\frac{169 \sqrt{3}}{4}\) на \(4\). Четверка в числителе и знаменателе сокращается: \(V = 169 \sqrt{3}\).
Таким образом, объем пирамиды равен \(169 \sqrt{3}\) кубических сантиметров.
Ответ: Объем пирамиды составляет \(169 \sqrt{3}\) см³.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!