ГДЗ по Геометрии 11 класс Номер 476 Атанасян — Подробные Ответы

Найдите объём наклонной треугольной призмы, если расстояния между её боковыми рёбрами равны 37 см, 13 см и 30 см, а площадь боковой поверхности равна 480 см\(^2\).

Объем наклонной призмы равен произведению площади сечения, перпендикулярного боковым ребрам, на длину бокового ребра, то есть \(V_{\text{призмы}} = S_{\text{сечения}} \cdot l\).

Сечением, перпендикулярным боковым ребрам, является треугольник со сторонами 37 см, 30 см и 13 см. Найдем площадь этого треугольника по формуле Герона. Полупериметр треугольника равен \(p = \frac{37+30+13}{2} = \frac{80}{2} = 40\) см. Площадь сечения равна \(S_{\text{сечения}} = \sqrt{p(p-a)(p-b)(p-c)} = \sqrt{40(40-37)(40-30)(40-13)} = \)
\(=\sqrt{40 \cdot 3 \cdot 10 \cdot 27} = \sqrt{32400} = 180\) см\(^2\). Площадь боковой поверхности призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра, то есть \(S_{\text{боковой}} = P_{\text{сечения}} \cdot l\). Периметр перпендикулярного сечения равен \(P_{\text{сечения}} = 37+30+13 = 80\) см. Длина бокового ребра равна \(l = \frac{S_{\text{боковой}}}{P_{\text{сечения}}} = \frac{480}{80} = 6\) см. Объем призмы равен \(V_{\text{призмы}} = S_{\text{сечения}} \cdot l = 180 \cdot 6 = 1080\) см\(^3\). Ответ: \(V_{\text{призмы}} = 1080\) см\(^3\).

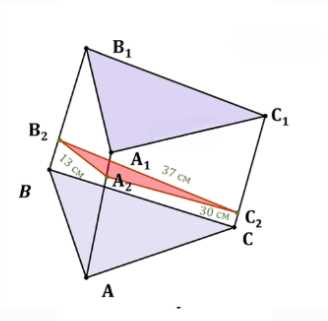
Дано: наклонная призма \(ABCA_1B_1C_1\), площадь боковой поверхности \(S_{\text{боковой}} = 480\) см\(^2\). Сечение \(A_2B_2C_2\) перпендикулярно боковым ребрам, при этом \(B_2C_2 \perp\) ребрам, \(A_2C_2 \perp\) ребрам, \(A_2B_2 \perp\) ребрам. Длины сторон этого перпендикулярного сечения равны \(B_2C_2 = 37\) см, \(A_2C_2 = 30\) см, \(B_2A_2 = 13\) см.

Найти: Объем призмы \(V_{\text{призмы}}\).

Решение: Объем наклонной призмы может быть найден как произведение площади сечения, перпендикулярного боковым ребрам, на длину бокового ребра. Это свойство призм известно и часто используется в стереометрии. Формула выглядит так: \(V_{\text{призмы}} = S_{\text{сечения}} \cdot l\), где \(S_{\text{сечения}}\) — площадь перпендикулярного сечения, а \(l\) — длина бокового ребра призмы.

В данной задаче перпендикулярным сечением является треугольник \(A_2B_2C_2\) со сторонами \(a = B_2C_2 = 37\) см, \(b = A_2C_2 = 30\) см и \(c = A_2B_2 = 13\) см. Для нахождения площади этого треугольника \(S_{\Delta A_2B_2C_2}\) воспользуемся формулой Герона. Сначала вычислим полупериметр \(p\) этого треугольника: \(p = \frac{a+b+c}{2} = \frac{37+30+13}{2} = \frac{80}{2} = 40\) см.

Теперь вычислим площадь треугольника \(A_2B_2C_2\) по формуле Герона: \(S_{\Delta A_2B_2C_2} = \sqrt{p(p-a)(p-b)(p-c)} = \sqrt{40(40-37)(40-30)(40-13)} = \)
\(=\sqrt{40 \cdot 3 \cdot 10 \cdot 27}\). Вычислим значение под корнем: \(40 \cdot 3 \cdot 10 \cdot 27 = (4 \cdot 10) \cdot 3 \cdot 10 \cdot (3 \cdot 9) = 4 \cdot 3 \cdot 9 \cdot 10 \cdot 10 \cdot 3 = \)
\(=(2^2) \cdot 3 \cdot (3^2) \cdot (10^2) \cdot 3 = 2^2 \cdot 3^4 \cdot 10^2 = (2 \cdot 3^2 \cdot 10)^2 = (2 \cdot 9 \cdot 10)^2 = \)
\(= (180)^2\).
Таким образом, площадь перпендикулярного сечения \(S_{\Delta A_2B_2C_2} = \sqrt{(180)^2} =180\) см\(^2\).

Площадь боковой поверхности призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра. Формула: \(S_{\text{боковой}} = P_{\text{сечения}} \cdot l\). Периметр перпендикулярного сечения \(P_{\Delta A_2B_2C_2}\) равен сумме длин его сторон: \(P_{\Delta A_2B_2C_2} = 37+30+13 = 80\) см.

Из формулы для площади боковой поверхности выразим длину бокового ребра \(l\): \(l = \frac{S_{\text{боковой}}}{P_{\text{сечения}}}\). Подставим известные значения: \(l = \frac{480}{80} = 6\) см.

Теперь, зная площадь перпендикулярного сечения и длину бокового ребра, мы можем найти объем призмы: \(V_{\text{призмы}} = S_{\Delta A_2B_2C_2} \cdot l = 180 \cdot 6\). Вычислим произведение: \(180 \cdot 6 = 1080\).

Следовательно, объем призмы равен 1080 см\(^3\).

Ответ: \(V_{\text{призмы}} = 1080\) см\(^3\).