ГДЗ по Геометрии 11 класс Номер 475 Атанасян — Подробные Ответы

Докажите, что объём наклонной призмы равен произведению бокового ребра на площадь сечения призмы плоскостью, перпендикулярной к боковым рёбрам и пересекающей их.

Приведем доказательство данного факта. Если разрезать предмет на части и сложить из него другой предмет, оба предмета будут иметь разную форму, но одинаковый объем. Проведем сечение, перпендикулярное ребру. Очевидно, что совместив две части, мы получим новую фигуру, прямую призму, с основанием, равным площади сечения \(S\), и высотой, равной длине бокового ребра \(l\). Объем прямой призмы равен произведению площади основания на высоту, то есть \(V_{\text{призмы прямой}} = S \cdot l\). Поскольку объем не изменился при преобразовании, объем исходной наклонной призмы также равен \(V_{\text{призмы}} = S \cdot l\), что и требовалось доказать. Ответ: \(V_{\text{призмы}} = S \cdot l\).

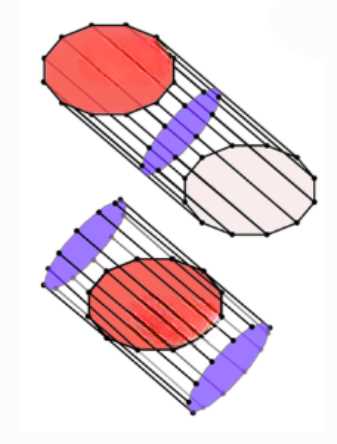
Рассмотрим наклонную призму с боковым ребром длиной \(l\). Проведем сечение плоскостью, перпендикулярной всем боковым ребрам этой призмы. Обозначим площадь этого сечения как \(S\). Требуется доказать, что объем призмы \(V_{\text{призмы}}\) равен произведению площади этого сечения на длину бокового ребра, то есть \(V_{\text{призмы}} = S \cdot l\).

Для доказательства воспользуемся принципом, который можно проиллюстрировать следующим образом: если тело разрезать на части и затем собрать эти части в другое тело, то объемы исходного и нового тел будут равны, независимо от их формы, при условии, что каждый «слой» или «срез» исходного тела соответствует «слою» или «срезу» нового тела с той же площадью. В данном случае мы можем «преобразовать» наклонную призму в прямую призму, не изменяя ее объема.

Представим, что мы «отрезаем» верхнюю часть наклонной призмы плоскостью, перпендикулярной боковым ребрам, проходящей через одну из вершин нижнего основания. Эта плоскость образует то самое сечение площадью \(S\). Оставшаяся нижняя часть призмы имеет одно основание и наклонную «крышу». Верхняя «отрезанная» часть представляет собой клин.

Теперь представим, что мы можем «сдвинуть» или «переместить» эту верхнюю «отрезанную» часть таким образом, чтобы ее наклонная «крыша» стала параллельна нижнему основанию исходной призмы, а плоскость сечения площадью \(S\) стала верхним основанием новой фигуры. При этом боковые ребра исходной призмы, имеющие длину \(l\), станут высотой новой фигуры, поскольку сечение было перпендикулярно этим ребрам.

В результате такого «перемещения» частей мы получим новую геометрическую фигуру. Основанием этой новой фигуры будет являться сечение площадью \(S\), которое мы провели перпендикулярно боковым ребрам. Боковые ребра исходной призмы, имеющие длину \(l\), станут перпендикулярны основанию новой фигуры, поскольку сечение было перпендикулярно им. Следовательно, новая фигура является прямой призмой.

Объем прямой призмы определяется как произведение площади ее основания на ее высоту. В нашем случае основанием новой прямой призмы является сечение площадью \(S\), а ее высота равна длине бокового ребра исходной наклонной призмы, то есть \(l\). Таким образом, объем новой прямой призмы равен \(V_{\text{прямой призмы}} = S \cdot l\).

Поскольку мы просто «пересобрали» части исходной наклонной призмы, не добавляя и не удаляя материал, объем новой прямой призмы равен объему исходной наклонной призмы. Следовательно, объем наклонной призмы равен \(V_{\text{призмы}} = V_{\text{прямой призмы}} = S \cdot l\).

Таким образом, доказано, что объем наклонной призмы равен произведению площади сечения, перпендикулярного боковым ребрам, на длину бокового ребра.

Ответ: \(V_{\text{призмы}} = S \cdot l\).