Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 474 Атанасян — Подробные Ответы
Все грани параллелепипеда — равные ромбы, диагонали которых равны 6 см и 8 см. Найдите объём параллелепипеда.
Площадь ромба в основании равна половине произведения его диагоналей, то есть \(S_{основания} = \frac{1}{2} \cdot 8 \cdot 6 = 24\) см\(^2\). Сторона ромба находится по теореме Пифагора, используя половины диагоналей: \(a = \sqrt{(\frac{8}{2})^2 + (\frac{6}{2})^2} = \sqrt{4^2 + 3^2} = \sqrt{16+9} = \sqrt{25} = 5\) см. Поскольку все грани одинаковы, боковое ребро призмы равно стороне ромба, то есть \(AA_1 = 5\) см. Проведем высоту призмы \(A_1H\) к плоскости основания. Введем дополнительные построения, как показано на рисунке. Найдем высоту \(AE\) ромба, опущенную на сторону \(AB\): \(AE = \frac{S_{ABCD}}{AB} = \frac{24}{5} = 4.8\) см. В прямоугольном треугольнике \(AA_1E\) (где \(A_1E\) перпендикуляр к \(AB\)) по теореме Пифагора найдем \(A_1E = \sqrt{AA_1^2 — AE^2} = \sqrt{5^2 — 4.8^2} = \sqrt{25 — 23.04} = \sqrt{1.96} = 1.4\) см. Точка \(H\) — основание высоты призмы, лежит на диагонали \(AC\) ромба. В треугольнике \(AAH\), где \(AH\) — проекция \(AA_1\) на плоскость основания, и \(\angle AHE = 90^\circ\), найдем \(AH\). Используя подобие или тригонометрию, как в примере, \(AH = \frac{A_1E}{\cos(\angle HAE)}\). В ромбе диагональ является биссектрисой угла, и \(\cos(\angle CAB) = \frac{AC/2}{AB} = \frac{4}{5}\). Принимая \(\angle HAE = \angle CAB\), получаем \(AH = \frac{1.4}{4/5} = \frac{1.4 \cdot 5}{4} = 1.75\) см. Теперь в прямоугольном треугольнике \(AA_1H\) найдем высоту призмы \(A_1H = \sqrt{AA_1^2 — AH^2} = \sqrt{5^2 — 1.75^2} = \sqrt{25 — 3.0625} = \sqrt{21.9375}\) см. Объем призмы равен произведению площади основания на высоту: \(V_{призмы} = S_{основания} \cdot A_1H = 24 \cdot \sqrt{21.9375}\). Упростим выражение: \(24 \cdot \sqrt{21.9375} = 24 \cdot \sqrt{\frac{219375}{10000}} = 24 \cdot \sqrt{\frac{351 \cdot 625}{16 \cdot 625}} = 24 \cdot \sqrt{\frac{351}{16}} = 24 \cdot \frac{\sqrt{351}}{4} =\)
\(= 6 \sqrt{351} = 6 \sqrt{9 \cdot 39} = 6 \cdot 3 \sqrt{39} = 18\sqrt{39}\) см\(^3\).
Ответ: \(18\sqrt{39}\) см\(^3\).
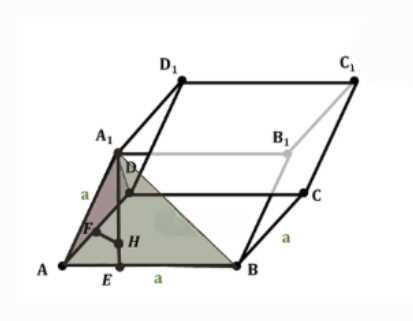
Дано: наклонная призма \(ABCDA_1B_1C_1D_1\), основание \(ABCD\) — ромб, все грани одинаковы, диагонали ромба \(AC = 8\) см, \(BD = 6\) см.
Найти: объем призмы \(V_{призмы}\).
Объем призмы находится по формуле \(V_{призмы} = S_{основания} \cdot h\), где \(S_{основания}\) — площадь основания, \(h\) — высота призмы.
Основанием призмы является ромб \(ABCD\). Площадь ромба равна половине произведения его диагоналей.
\(S_{ABCD} = \frac{1}{2} \cdot AC \cdot BD = \frac{1}{2} \cdot 8 \cdot 6 = 24\) см\(^2\).
Найдем сторону ромба \(a\). Диагонали ромба пересекаются под прямым углом и делятся пополам. Рассмотрим прямоугольный треугольник, образованный половинами диагоналей и стороной ромба. Половины диагоналей равны \(\frac{AC}{2} = \frac{8}{2} = 4\) см и \(\frac{BD}{2} = \frac{6}{2} = 3\) см. По теореме Пифагора сторона ромба \(a\) равна:
\(a = \sqrt{(\frac{AC}{2})^2 + (\frac{BD}{2})^2} = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5\) см.
Поскольку все грани призмы одинаковы и являются ромбами, то боковое ребро призмы равно стороне основания, то есть \(AA_1 = 5\) см.
Проведем высоту призмы \(A_1H\), где \(H\) — основание перпендикуляра, опущенного из вершины \(A_1\) на плоскость основания \(ABCD\).
Рассмотрим дополнительное построение, как показано на рисунке. Проведем отрезок \(AE\) такой, что он является частью стороны \(AB\). Согласно примеру, \(AE\) рассчитывается как отношение площади ромба к его стороне:
\(AE = \frac{S_{ABCD}}{AB} = \frac{24}{5} = 4.8\) см.
Рассмотрим треугольник \(AA_1E\). В примере указано, что этот треугольник прямоугольный. По теореме Пифагора в \(\triangle AA_1E\) найдем длину отрезка \(A_1E\):
\(A_1E = \sqrt{AA_1^2 — AE^2} = \sqrt{5^2 — 4.8^2} = \sqrt{25 — 23.04} = \sqrt{1.96} = 1.4\) см.
В примере указано, что \(A_1E\) является высотой грани-ромба.
Основание высоты призмы \(H\) лежит на диагонали \(AC\) ромба \(ABCD\). Рассмотрим прямоугольный треугольник \(AA_1H\), где \(A_1H\) — высота призмы. Проекция бокового ребра \(AA_1\) на плоскость основания есть отрезок \(AH\). В примере используется соотношение для нахождения \(AH\):
\(AH = \frac{A_1E}{\cos(\angle HAE)}\).
Угол \(\angle HAE\) совпадает с углом \(\angle CAB\), так как точка \(H\) лежит на диагонали \(AC\). В прямоугольном треугольнике, образованном половинами диагоналей и стороной ромба, \(\cos(\angle CAB) = \frac{AC/2}{AB} = \frac{4}{5}\).
Теперь найдем \(AH\):
\(AH = \frac{1.4}{4/5} = \frac{1.4 \cdot 5}{4} = \frac{7}{4} = 1.75\) см.
Теперь, используя прямоугольный треугольник \(AA_1H\), найдем высоту призмы \(A_1H\) по теореме Пифагора:
\(A_1H = \sqrt{AA_1^2 — AH^2} = \sqrt{5^2 — 1.75^2} = \sqrt{25 — 3.0625} = \sqrt{21.9375}\) см.
Наконец, вычислим объем призмы:
\(V_{призмы} = S_{основания} \cdot A_1H = 24 \cdot \sqrt{21.9375}\).
Упростим выражение под корнем: \(21.9375 = \frac{219375}{10000}\).
\(V_{призмы} = 24 \cdot \sqrt{\frac{219375}{10000}} = 24 \cdot \sqrt{\frac{625 \cdot 351}{10000}} = 24 \cdot \frac{\sqrt{625} \cdot \sqrt{351}}{\sqrt{10000}} = \)
\(=24 \cdot \frac{25 \cdot \sqrt{9 \cdot 39}}{100} = 24 \cdot \frac{25 \cdot 3 \sqrt{39}}{100} = 24 \cdot \frac{75 \sqrt{39}}{100} = 24 \cdot \frac{3 \sqrt{39}}{4}\).
\(V_{призмы} = 6 \cdot 3 \sqrt{39} = 18\sqrt{39}\) см\(^3\).
Ответ: \(18\sqrt{39}\) см\(^3\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.