
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 473 Атанасян — Подробные Ответы
Основанием наклонного параллелепипеда является прямоугольник со сторонами \(a\) и \(b\). Боковое ребро длины \(c\) составляет со смежными сторонами основания углы, равные \(\phi\). Найдите объём параллелепипеда.
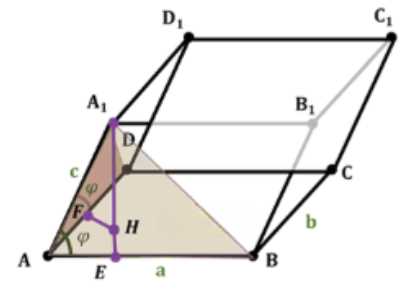
Объём наклонной призмы равен произведению площади основания на высоту. Основанием является прямоугольник ABCD с площадью \(S_{ABCD} = AB \cdot AD = a \cdot b\). Высота призмы \(A_1H\) может быть найдена из прямоугольного треугольника \(AA_1H\), где \(AA_1 = c\). Проведем перпендикуляры \(A_1E \perp AB\) и \(A_1F \perp AD\). По теореме о трех перпендикулярах \(AE\) и \(AF\) являются проекциями \(AA_1\) на плоскость основания. В прямоугольных треугольниках \(AA_1E\) и \(AA_1F\) имеем \(AE = AA_1 \cos(\phi) = c \cos(\phi)\) и \(AF = AA_1 \cos(\phi) = c \cos(\phi)\). Поскольку ABCD — прямоугольник, \(\angle DAB = 90^\circ\). Треугольник \(AEF\) является равнобедренным прямоугольным треугольником с прямым углом при A. Точка H, основание высоты \(A_1H\), лежит на биссектрисе угла \(DAB\), поэтому \(\angle EAH = \angle FAH = 45^\circ\). В прямоугольном треугольнике \(AFH\) имеем \(AH = \frac{AF}{\cos(45^\circ)} = \frac{c \cos(\phi)}{1/\sqrt{2}} = \sqrt{2} c \cos(\phi)\). Теперь в прямоугольном треугольнике \(AA_1H\) по теореме Пифагора находим высоту \(A_1H = \sqrt{AA_1^2 — AH^2} = \sqrt{c^2 — (\sqrt{2} c \cos(\phi))^2} = \sqrt{c^2 — 2c^2 \cos^2(\phi)} = \)
\(=\sqrt{c^2(1 — 2\cos^2(\phi))}\). Используя тригонометрическую формулу \(1 — 2\cos^2(\phi) = -(2\cos^2(\phi) — 1) = -\cos(2\phi)\), получаем \(A_1H = \sqrt{c^2(-\cos(2\phi))} = c \sqrt{-\cos(2\phi)}\). Для существования действительного значения высоты необходимо, чтобы \(-\cos(2\phi) \ge 0\), то есть \(\cos(2\phi) \le 0\). Объём призмы равен \(V_{призмы} = S_{ABCD} \cdot A_1H = a \cdot b \cdot c \sqrt{-\cos(2\phi)}\).
Дано наклонная призма \(ABCDA_1B_1C_1D_1\). Основание \(ABCD\) является прямоугольником со сторонами \(AB = a\) и \(AD = b\). Боковое ребро \(AA_1\) имеет длину \(c\). Углы между боковым ребром \(AA_1\) и смежными сторонами основания \(AB\) и \(AD\) равны \(\angle A_1AB = \phi\) и \(\angle A_1AD = \phi\). Необходимо найти объём призмы \(V_{призмы}\).
Объём любой призмы равен произведению площади её основания на высоту. В данном случае основанием является прямоугольник \(ABCD\), площадь которого равна \(S_{ABCD} = AB \cdot AD = a \cdot b\). Высотой призмы является длина перпендикуляра, опущенного из любой точки верхнего основания на плоскость нижнего основания. Построим высоту призмы \(A_1H\), где \(H\) — основание перпендикуляра, опущенного из точки \(A_1\) на плоскость основания \(ABCD\). Тогда объём призмы будет равен \(V_{призмы} = S_{ABCD} \cdot A_1H = a \cdot b \cdot A_1H\).
Для нахождения высоты \(A_1H\) рассмотрим положение точки \(H\) в плоскости основания. Проведем из точки \(A_1\) перпендикуляры \(A_1E\) к прямой \(AB\) и \(A_1F\) к прямой \(AD\). По определению, \(A_1E \perp AB\) и \(A_1F \perp AD\). По теореме о трех перпендикулярах, если наклонная \(A_1E\) перпендикулярна прямой \(AB\) в плоскости, то и её проекция \(AE\) на эту плоскость перпендикулярна \(AB\). Аналогично, \(AF\) является проекцией \(A_1F\) на плоскость основания и \(AF \perp AD\).
В прямоугольном треугольнике \(AA_1E\) с гипотенузой \(AA_1 = c\) и углом \(\angle A_1AB = \phi\) прилежащий катет \(AE\) равен \(AA_1 \cos(\phi) = c \cos(\phi)\). В прямоугольном треугольнике \(AA_1F\) с гипотенузой \(AA_1 = c\) и углом \(\angle A_1AD = \phi\) прилежащий катет \(AF\) равен \(AA_1 \cos(\phi) = c \cos(\phi)\). Таким образом, \(AE = AF = c \cos(\phi)\).
Поскольку \(ABCD\) — прямоугольник, \(\angle DAB = 90^\circ\). Точка \(H\), основание перпендикуляра \(A_1H\), является проекцией точки \(A_1\) на плоскость основания. Вектор \(AH\) является проекцией вектора \(AA_1\) на плоскость основания. Поскольку углы \(\angle A_1AB\) и \(\angle A_1AD\) равны, и \(AE\) и \(AF\) являются проекциями отрезков \(AA_1\) вдоль направлений \(AB\) и \(AD\) соответственно (точнее, \(AE\) и \(AF\) — это длины проекций отрезка \(AA_1\) на прямые \(AB\) и \(AD\)), а \(AE = AF\), точка \(H\) лежит на биссектрисе угла \(DAB\). Следовательно, \(\angle EAH = \angle FAH = \frac{\angle DAB}{2} = \frac{90^\circ}{2} = 45^\circ\).
Рассмотрим прямоугольный треугольник \(AFH\). В нем катет \(AF = c \cos(\phi)\) и угол \(\angle FAH = 45^\circ\). Гипотенуза \(AH\) может быть найдена с использованием косинуса угла: \(AH = \frac{AF}{\cos(\angle FAH)} = \frac{c \cos(\phi)}{\cos(45^\circ)} = \frac{c \cos(\phi)}{1/\sqrt{2}} = \sqrt{2} c \cos(\phi)\).
Теперь рассмотрим прямоугольный треугольник \(AA_1H\). Гипотенуза этого треугольника равна \(AA_1 = c\), а один из катетов равен \(AH = \sqrt{2} c \cos(\phi)\). Высота призмы \(A_1H\) является другим катетом. По теореме Пифагора имеем \(A_1H^2 = AA_1^2 — AH^2 = c^2 — (\sqrt{2} c \cos(\phi))^2 = c^2 — 2c^2 \cos^2(\phi) = c^2(1 — 2\cos^2(\phi))\).
Из тригонометрии известно, что \(1 — 2\cos^2(\phi) = -(2\cos^2(\phi) — 1) = -\cos(2\phi)\). Подставляя это в выражение для \(A_1H^2\), получаем \(A_1H^2 = c^2(-\cos(2\phi))\). Следовательно, высота призмы равна \(A_1H = \sqrt{c^2(-\cos(2\phi))} = c \sqrt{-\cos(2\phi)}\). Для того чтобы высота была действительным числом, подкоренное выражение должно быть неотрицательным, то есть \(-\cos(2\phi) \ge 0\), что эквивалентно \(\cos(2\phi) \le 0\).
Наконец, подставим найденное значение высоты \(A_1H\) и площадь основания \(S_{ABCD}\) в формулу объёма призмы: \(V_{призмы} = S_{ABCD} \cdot A_1H = (a \cdot b) \cdot (c \sqrt{-\cos(2\phi)}) = a \cdot b \cdot c \sqrt{-\cos(2\phi)}\).
Таким образом, объём наклонной призмы равен \(a \cdot b \cdot c \sqrt{-\cos(2\phi)}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!