Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 470 Атанасян — Подробные Ответы
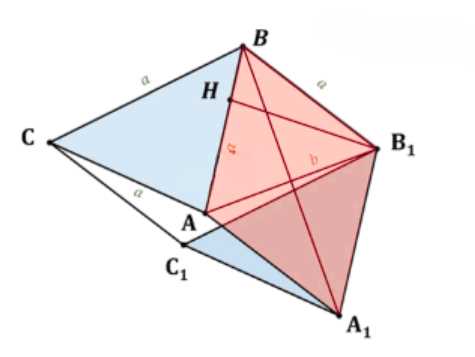
Найдите объём наклонной призмы \(ABCA_1B_1C_1\), если \(AB = BC = СА = a\), \(АВВ_1А_1\) — ромб, \(АВ_1 < ВА_1\), \(AB_1 = b\), двугранный угол с ребром АВ прямой.
Объем призмы равен произведению площади основания на высоту призмы \(V_{призмы} = S_{основания} \cdot h\). Основанием является равносторонний треугольник \(ABC\) со стороной \(a\), поэтому площадь основания \(S_{основания} = S_{\triangle ABC} = \frac{\sqrt{3}}{4} a^2\). Высота призмы \(h\) в данном случае равна высоте ромба \(ABB_1A_1\), опущенной из вершины \(B_1\) на сторону AB, так как двугранный угол с ребром AB прямой. Обозначим эту высоту \(B_1H\).
Площадь треугольника \(ABB_1\) со сторонами \(a, a, b\) по формуле Герона равна \(S_{\triangle ABB_1} = \frac{b}{2} \sqrt{a^2 — (\frac{b}{2})^2}\).
Также, площадь треугольника \(ABB_1\) равна \(\frac{1}{2} \cdot AB \cdot B_1H = \frac{1}{2} a \cdot B_1H\).
Приравнивая эти выражения, получаем \(\frac{1}{2} a \cdot B_1H = \frac{b}{2} \sqrt{a^2 — \frac{b^2}{4}}\), откуда \(B_1H = \frac{b}{a} \sqrt{a^2 — \frac{b^2}{4}}\).
Объем призмы \(V_{призмы} = S_{\triangle ABC} \cdot B_1H = \frac{\sqrt{3}}{4} a^2 \cdot \frac{b}{a} \sqrt{a^2 — \frac{b^2}{4}}\).
Упрощая, получаем \(V_{призмы} = \frac{\sqrt{3}}{4} ab \sqrt{\frac{4a^2 — b^2}{4}} = \frac{\sqrt{3}}{4} ab \frac{\sqrt{4a^2 — b^2}}{2} = \frac{\sqrt{3} ab \sqrt{4a^2 — b^2}}{8}\).
Преобразуя выражение под корнем, \(\sqrt{4a^2 — b^2} = \frac{1}{\sqrt{3}} \sqrt{12a^2 — 3b^2}\).
Следовательно, \(V_{призмы} = \frac{\sqrt{3} ab}{8} \cdot \frac{1}{\sqrt{3}} \sqrt{12a^2 — 3b^2} = \frac{ab}{8} \sqrt{12a^2 — 3b^2}\).
Ответ: \(V_{призмы} = \frac{ab}{8} \sqrt{12a^2 — 3b^2}\).
Дано: наклонная призма \(ABCA_1B_1C_1\), \(AB = BC = CA = a\), \(АВВ_1А_1\) — ромб, \(АВ_1 < ВА_1\), \(AB_1 = b\), двугранный угол с ребром AB прямой.
Найти: объем призмы \(V_{призмы}\). Объем призмы находится по формуле \(V_{призмы} = S_{основания} \cdot h\), где \(S_{основания}\) - площадь основания призмы, а \(h\) - высота призмы. Основанием призмы является треугольник \(ABC\). По условию \(AB = BC = CA = a\), следовательно, треугольник \(ABC\) является равносторонним. Площадь равностороннего треугольника со стороной \(a\) вычисляется по формуле \(S_{\triangle ABC} = \frac{\sqrt{3}}{4} a^2\). Высота призмы - это расстояние между плоскостями основания \(ABC\) и \(A_1B_1C_1\). В данном случае, поскольку двугранный угол с ребром \(AB\) прямой, высота призмы совпадает с высотой ромба \(ABB_1A_1\), опущенной из вершины \(B_1\) на сторону \(AB\). Обозначим эту высоту \(B_1H\). Рассмотрим ромб \(ABB_1A_1\). Так как это ромб, все его стороны равны. По условию \(AB = a\), следовательно, \(AA_1 = BB_1 = A_1B_1 = a\). Диагональ ромба \(AB_1 = b\).
Рассмотрим треугольник \(ABB_1\). Его стороны равны \(AB = a\), \(BB_1 = a\), и \(AB_1 = b\). Мы можем найти площадь этого треугольника двумя способами.
Первый способ: используя формулу Герона. Полупериметр треугольника \(ABB_1\) равен \(p = \frac{AB + BB_1 + AB_1}{2} = \frac{a + a + b}{2} = \frac{2a + b}{2} = a + \frac{b}{2}\).
Площадь треугольника \(ABB_1\) по формуле Герона:
\(S_{\triangle ABB_1} = \sqrt{p(p - AB)(p - BB_1)(p - AB_1)}\)
\(S_{\triangle ABB_1} = \sqrt{(a + \frac{b}{2})(a + \frac{b}{2} - a)(a + \frac{b}{2} - a)(a + \frac{b}{2} - b)}\)
\(S_{\triangle ABB_1} = \sqrt{(a + \frac{b}{2})(\frac{b}{2})(\frac{b}{2})(a - \frac{b}{2})}\)
\(S_{\triangle ABB_1} = \sqrt{(a + \frac{b}{2})(a - \frac{b}{2})(\frac{b}{2})^2}\)
\(S_{\triangle ABB_1} = \sqrt{(a^2 - (\frac{b}{2})^2)(\frac{b}{2})^2}\)
\(S_{\triangle ABB_1} = \sqrt{(a^2 - \frac{b^2}{4}) \frac{b^2}{4}}\)
\(S_{\triangle ABB_1} = \frac{b}{2} \sqrt{a^2 - \frac{b^2}{4}}\) Второй способ: используя формулу площади через основание и высоту. Площадь треугольника \(ABB_1\) также равна \(\frac{1}{2} \cdot AB \cdot B_1H\), где \(B_1H\) - высота, опущенная из \(B_1\) на \(AB\).
\(S_{\triangle ABB_1} = \frac{1}{2} a \cdot B_1H\) Приравниваем два выражения для площади треугольника \(ABB_1\):
\(\frac{1}{2} a \cdot B_1H = \frac{b}{2} \sqrt{a^2 - \frac{b^2}{4}}\)
Умножим обе части на 2:
\(a \cdot B_1H = b \sqrt{a^2 - \frac{b^2}{4}}\)
Выразим высоту \(B_1H\):
\(B_1H = \frac{b}{a} \sqrt{a^2 - \frac{b^2}{4}}\) Теперь подставим площадь основания и высоту призмы в формулу объема:
\(V_{призмы} = S_{\triangle ABC} \cdot B_1H\)
\(V_{призмы} = \frac{\sqrt{3}}{4} a^2 \cdot \frac{b}{a} \sqrt{a^2 - \frac{b^2}{4}}\)
Сократим \(a\):
\(V_{призмы} = \frac{\sqrt{3}}{4} ab \sqrt{a^2 - \frac{b^2}{4}}\)
Преобразуем выражение под корнем:
\(a^2 - \frac{b^2}{4} = \frac{4a^2 - b^2}{4}\)
\(V_{призмы} = \frac{\sqrt{3}}{4} ab \sqrt{\frac{4a^2 - b^2}{4}}\)
\(V_{призмы} = \frac{\sqrt{3}}{4} ab \frac{\sqrt{4a^2 - b^2}}{\sqrt{4}}\)
\(V_{призмы} = \frac{\sqrt{3}}{4} ab \frac{\sqrt{4a^2 - b^2}}{2}\)
\(V_{призмы} = \frac{\sqrt{3} ab \sqrt{4a^2 - b^2}}{8}\)
Мы можем внести \(\sqrt{3}\) под корень, умножив выражение под корнем на 3:
\(\sqrt{3} \sqrt{4a^2 - b^2} = \sqrt{3(4a^2 - b^2)} = \sqrt{12a^2 - 3b^2}\)
Следовательно,
\(V_{призмы} = \frac{ab}{8} \sqrt{12a^2 - 3b^2}\) Ответ: \(V_{призмы} = \frac{ab}{8} \sqrt{12a^2 - 3b^2}\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.