
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 469 Атанасян — Подробные Ответы
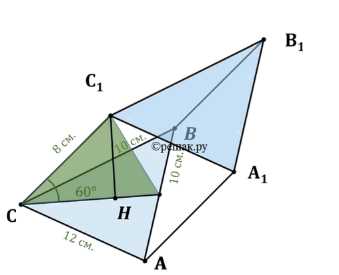
Найдите объём наклонной призмы, у которой основанием является треугольник со сторонами 10 см, 10 см и 12 см, а боковое ребро, равное 8 см, составляет с плоскостью основания угол в 60°
Площадь основания найдем по формуле Герона. Полупериметр треугольника равен \(p = \frac{10+10+12}{2} = 16\) см. Площадь основания \(S_{основания} = \sqrt{16(16-10)(16-10)(16-12)} = \sqrt{16 \cdot 6 \cdot 6 \cdot 4} = \sqrt{2304} = 48\) см\(^2\). Высота призмы \(h\) равна произведению длины бокового ребра на синус угла между боковым ребром и плоскостью основания. \(h = 8 \cdot \sin(60^\circ) = 8 \cdot \frac{\sqrt{3}}{2} = 4\sqrt{3}\) см. Объем призмы равен произведению площади основания на высоту: \(V_{призмы} = S_{основания} \cdot h = 48 \cdot 4\sqrt{3} = 192\sqrt{3}\) см\(^3\). Ответ: \(192\sqrt{3}\) см\(^3\).
Объем наклонной призмы равен произведению площади основания на высоту. Формула для объема призмы: \(V = S_{основания} \cdot h\).
Сначала найдем площадь основания призмы. Основанием является треугольник со сторонами 10 см, 10 см и 12 см. Для нахождения площади этого треугольника воспользуемся формулой Герона. Формула Герона для площади треугольника со сторонами \(a\), \(b\), \(c\) и полупериметром \(p\) имеет вид \(S = \sqrt{p(p-a)(p-b)(p-c)}\).
Вычислим полупериметр \(p\) треугольника: \(p = \frac{10+10+12}{2} = \frac{32}{2} = 16\) см.
Теперь подставим значения сторон и полупериметра в формулу Герона для нахождения площади основания \(S_{основания}\): \(S_{основания} = \sqrt{16(16-10)(16-10)(16-12)} = \sqrt{16 \cdot 6 \cdot 6 \cdot 4}\). Вычисляем значение под корнем: \(16 \cdot 6 \cdot 6 \cdot 4 = 576 \cdot 4 = 2304\). Тогда площадь основания \(S_{основания} = \sqrt{2304} = 48\) см\(^2\).
Далее найдем высоту призмы \(h\). Высота наклонной призмы равна произведению длины бокового ребра на синус угла между боковым ребром и плоскостью основания. Длина бокового ребра равна 8 см, а угол между боковым ребром и плоскостью основания равен 60°. Таким образом, высота призмы \(h = 8 \cdot \sin(60^\circ)\). Значение синуса 60° равно \(\frac{\sqrt{3}}{2}\). Следовательно, высота призмы \(h = 8 \cdot \frac{\sqrt{3}}{2} = 4\sqrt{3}\) см.
Теперь, зная площадь основания и высоту призмы, мы можем вычислить ее объем по формуле \(V = S_{основания} \cdot h\). Подставляем найденные значения: \(V_{призмы} = 48 \cdot 4\sqrt{3}\). Выполняем умножение: \(48 \cdot 4 = 192\). Таким образом, объем призмы \(V_{призмы} = 192\sqrt{3}\) см\(^3\).
Ответ: \(192\sqrt{3}\) см\(^3\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!