
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 467 Атанасян — Подробные Ответы
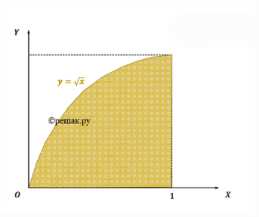
Фигура, заштрихованная на рисунке 147, вращается вокруг оси Ох. Найдите объём полученного тела.
Объем фигуры вращения находится по формуле \(V = \int_{a}^{b} \pi [f(x)]^2 dx\). В данном случае \(f(x) = \sqrt{x}\), \(a = 0\), \(b = 1\). Подставляя значения в формулу, получаем \(V = \int_{0}^{1} \pi (\sqrt{x})^2 dx\). Упрощая, имеем \(V = \int_{0}^{1} \pi x dx\). Интегрируя, получаем \(V = \pi \left[ \frac{x^2}{2} \right]_{0}^{1}\). Вычисляя определенный интеграл от 0 до 1, находим \(V = \pi \left( \frac{1^2}{2} — \frac{0^2}{2} \right) = \pi \left( \frac{1}{2} — 0 \right) = \frac{\pi}{2}\). Ответ: \(V_{\text{фигуры}} = \frac{\pi}{2}\).
Для нахождения объема фигуры вращения, образованной вращением области под графиком функции \(y = f(x)\) от \(x=a\) до \(x=b\) вокруг оси Ох, используется формула дисков: \(V = \int_{a}^{b} \pi [f(x)]^2 dx\).
В данной задаче область ограничена кривой \(y = \sqrt{x}\), осью Ох и прямой \(x = 1\). Фигура вращается вокруг оси Ох.
Следовательно, функция \(f(x) = \sqrt{x}\).
Пределы интегрирования определяются по оси Ох. Левая граница области находится в точке \(x=0\) (начало координат), а правая граница задана прямой \(x=1\). Таким образом, нижний предел интегрирования \(a = 0\), а верхний предел интегрирования \(b = 1\).
Подставляем эти значения в формулу для объема:
\(V = \int_{0}^{1} \pi [\sqrt{x}]^2 dx\).
Теперь упростим подынтегральное выражение. Квадратный корень в квадрате равен самому числу (для неотрицательных значений x, что выполняется в пределах от 0 до 1): \((\sqrt{x})^2 = x\).
Таким образом, интеграл принимает вид:
\(V = \int_{0}^{1} \pi x dx\).
Константу \(\pi\) можно вынести за знак интеграла:
\(V = \pi \int_{0}^{1} x dx\).
Далее необходимо вычислить определенный интеграл от функции \(x\) по переменной \(x\) в пределах от 0 до 1. Первообразной для функции \(x\) является \(\frac{x^2}{2}\).
Согласно формуле Ньютона-Лейбница, определенный интеграл вычисляется как разность значений первообразной в верхнем и нижнем пределах интегрирования:
\(\int_{0}^{1} x dx = \left[ \frac{x^2}{2} \right]_{0}^{1} = \frac{1^2}{2} — \frac{0^2}{2}\).
Вычисляем значения:
\(\frac{1^2}{2} = \frac{1}{2}\).
\(\frac{0^2}{2} = 0\).
Разность равна \(\frac{1}{2} — 0 = \frac{1}{2}\).
Теперь умножим полученное значение определенного интеграла на константу \(\pi\), которую мы вынесли ранее:
\(V = \pi \times \frac{1}{2} = \frac{\pi}{2}\).
Следовательно, объем фигуры вращения равен \(\frac{\pi}{2}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!