
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 462 Атанасян — Подробные Ответы
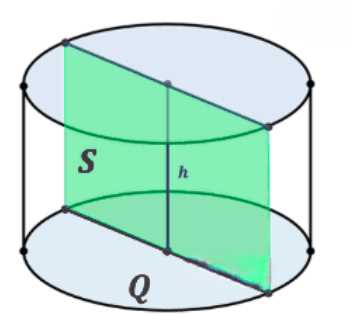
Площадь основания цилиндра равна \(Q\), а площадь его осевого сечения равна \(S\). Найдите объём цилиндра.
Дано: цилиндр, \(S_{\text{основания}} = Q\), \(S_{\text{осевого сечения}} = S\). Найти: \(V_{\text{цилиндра}}\).
Осевое сечение цилиндра — прямоугольник. Площадь осевого сечения равна произведению диаметра основания на высоту: \(S_{\text{осевого сечения}} = d \cdot h\).
Площадь основания цилиндра равна \(S_{\text{основания}} = \pi r^2 = \frac{\pi d^2}{4}\).
Из \(S = d \cdot h\) выразим диаметр \(d = \frac{S}{h}\).
Подставим выражение для диаметра в формулу площади основания: \(Q = \frac{\pi (\frac{S}{h})^2}{4} = \frac{\pi S^2}{4h^2}\).
Выразим высоту \(h\) из полученного уравнения: \(4Qh^2 = \pi S^2\), откуда \(h^2 = \frac{\pi S^2}{4Q}\), и \(h = \sqrt{\frac{\pi S^2}{4Q}} = \frac{S\sqrt{\pi}}{2\sqrt{Q}}\).
Объём цилиндра равен произведению площади основания на высоту: \(V_{\text{цилиндра}} = S_{\text{основания}} \cdot h = Q \cdot h\).
Подставим найденное выражение для \(h\): \(V_{\text{цилиндра}} = Q \cdot \frac{S\sqrt{\pi}}{2\sqrt{Q}} = \frac{Q S\sqrt{\pi}}{2\sqrt{Q}} = \frac{\sqrt{Q}\sqrt{Q} S\sqrt{\pi}}{2\sqrt{Q}} = \frac{S\sqrt{\pi Q}}{2}\).
Ответ: \(V_{\text{цилиндра}} = \frac{S\sqrt{\pi Q}}{2}\).
Решение задачи.
Дано: цилиндр, площадь основания которого \(S_{\text{основания}}\) равна \(Q\), а площадь осевого сечения \(S_{\text{осевого сечения}}\) равна \(S\). Требуется найти объём цилиндра \(V_{\text{цилиндра}}\).
Решение:
Осевое сечение цилиндра представляет собой прямоугольник. Стороны этого прямоугольника — это диаметр основания цилиндра \(d\) и его высота \(h\). Следовательно, площадь осевого сечения \(S_{\text{осевого сечения}}\) выражается формулой \(S = d \cdot h\).
Площадь основания цилиндра \(S_{\text{основания}}\) вычисляется по формуле площади круга: \(S_{\text{основания}} = \pi r^2\), где \(r\) — радиус основания. Поскольку диаметр \(d\) в два раза больше радиуса \(r\), то \(d = 2r\), или \(r = \frac{d}{2}\). Подставляя это в формулу площади основания, получаем \(Q = \pi \left(\frac{d}{2}\right)^2 = \pi \frac{d^2}{4}\).
Таким образом, у нас есть система из двух уравнений, связывающих известные величины \(S\) и \(Q\) с неизвестными \(d\) и \(h\):
\(S = d \cdot h\)
\(Q = \frac{\pi d^2}{4}\)
Наша цель — найти объём цилиндра \(V_{\text{цилиндра}}\). Объём цилиндра равен произведению площади основания на высоту: \(V_{\text{цилиндра}} = S_{\text{основания}} \cdot h\). Поскольку \(S_{\text{основания}} = Q\), формула для объёма принимает вид \(V_{\text{цилиндра}} = Q \cdot h\). Для нахождения объёма нам необходимо выразить высоту \(h\) через известные величины \(S\) и \(Q\).
Из первого уравнения \(S = d \cdot h\) выразим диаметр \(d\): \(d = \frac{S}{h}\).
Теперь подставим это выражение для \(d\) во второе уравнение \(Q = \frac{\pi d^2}{4}\):
\(Q = \frac{\pi \left(\frac{S}{h}\right)^2}{4}\)
Возведем дробь в скобках в квадрат:
\(Q = \frac{\pi \frac{S^2}{h^2}}{4}\)
Умножим числитель на \(\pi\) и разделим на 4:
\(Q = \frac{\pi S^2}{4h^2}\)
Мы получили уравнение, связывающее \(Q\), \(S\), и \(h\). Теперь выразим \(h\) из этого уравнения. Умножим обе части уравнения на \(4h^2\):
\(4Qh^2 = \pi S^2\)
Разделим обе части на \(4Q\) (поскольку \(Q\) — площадь, она положительна, и деление возможно):
\(h^2 = \frac{\pi S^2}{4Q}\)
Извлечем квадратный корень из обеих частей уравнения, чтобы найти \(h\). Поскольку высота цилиндра положительна, берем положительный корень:
\(h = \sqrt{\frac{\pi S^2}{4Q}}\)
Разобьем корень на корни числителя и знаменателя:
\(h = \frac{\sqrt{\pi S^2}}{\sqrt{4Q}}\)
Извлечем корни из выражений в числителе и знаменателе:
\(h = \frac{S\sqrt{\pi}}{2\sqrt{Q}}\)
Теперь, когда мы выразили высоту \(h\) через \(S\) и \(Q\), подставим это выражение в формулу объёма цилиндра \(V_{\text{цилиндра}} = Q \cdot h\):
\(V_{\text{цилиндра}} = Q \cdot \frac{S\sqrt{\pi}}{2\sqrt{Q}}\)
Для упрощения выражения заметим, что \(Q = (\sqrt{Q})^2 = \sqrt{Q} \cdot \sqrt{Q}\). Подставим это в формулу объёма:
\(V_{\text{цилиндра}} = \frac{\sqrt{Q} \cdot \sqrt{Q} \cdot S\sqrt{\pi}}{2\sqrt{Q}}\)
Сократим \(\sqrt{Q}\) в числителе и знаменателе:
\(V_{\text{цилиндра}} = \frac{\sqrt{Q} S\sqrt{\pi}}{2}\)
Перегруппируем множители под корнем в числителе:
\(V_{\text{цилиндра}} = \frac{S\sqrt{\pi Q}}{2}\)
Таким образом, объём цилиндра выражается через площади его основания и осевого сечения по формуле \(V_{\text{цилиндра}} = \frac{S\sqrt{\pi Q}}{2}\).
Ответ: \(V_{\text{цилиндра}} = \frac{S\sqrt{\pi Q}}{2}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!