
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 461 Атанасян — Подробные Ответы
Какое количество нефти (в тоннах) вмещает цилиндрическая цистерна диаметром 18 м и высотой 7 м, если плотность нефти равна 0,85 г/см\(^3\)?
Дано: \(h = 7\) м, \(d = 18\) м, \(\rho = 0.85\) г/см\(^3\). Найти: \(m\). Цистерна имеет форму цилиндра. Объем цилиндра находится по формуле \(V = \pi \frac{d^2}{4} h\). Масса находится по формуле \(m = \rho V\). Переведем единицы: \(h = 7\) м = \(700\) см, \(d = 18\) м = \(1800\) см. Тогда \(V = \pi \frac{(1800 \text{ см})^2}{4} \times 700 \text{ см}\). Масса нефти \(m = 0.85 \text{ г/см}^3 \times \pi \frac{(1800 \text{ см})^2}{4} \times 700 \text{ см} = 1514090579\) г.
Переведем в тонны: \(m = \frac{1514090579}{1000000}\) т = \(1514.09\) т. Ответ: \(1514,09\) т.
Дано: высота цистерны \(h = 7\) м, диаметр цистерны \(d = 18\) м, плотность нефти \(\rho = 0.85\) г/см\(^3\).
Найти: масса нефти \(m\).
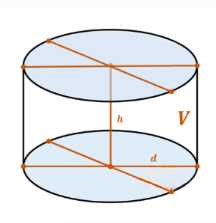
Цистерна имеет форму цилиндра. Для нахождения массы нефти необходимо сначала найти объем цистерны, а затем умножить его на плотность нефти.
Формула для объема цилиндра: \(V = S_{\text{основания}} \times h\), где \(S_{\text{основания}}\) — площадь основания цилиндра, а \(h\) — его высота. Основание цилиндра представляет собой круг. Площадь круга находится по формуле \(S_{\text{основания}} = \pi r^2\), где \(r\) — радиус круга. Поскольку радиус равен половине диаметра \(r = \frac{d}{2}\), площадь основания можно выразить через диаметр: \(S_{\text{основания}} = \pi \left(\frac{d}{2}\right)^2 = \pi \frac{d^2}{4}\).
Следовательно, объем цилиндра равен \(V = \pi \frac{d^2}{4} h\).
Формула, связывающая массу, плотность и объем: \(m = \rho V\).
Перед проведением расчетов необходимо убедиться, что все величины выражены в согласованных единицах измерения. Плотность дана в г/см\(^3\), а высота и диаметр — в метрах. Переведем высоту и диаметр в сантиметры, зная, что \(1\) м = \(100\) см.
Высота цистерны в сантиметрах: \(h = 7\) м \(= 7 \times 100\) см \(= 700\) см.
Диаметр цистерны в сантиметрах: \(d = 18\) м \(= 18 \times 100\) см \(= 1800\) см.
Теперь подставим значения диаметра и высоты в сантиметрах в формулу для объема цилиндра:
\(V = \pi \frac{(1800 \text{ см})^2}{4} \times 700 \text{ см}\).
Далее подставим значение объема и плотности в формулу для массы:
\(m = 0.85 \text{ г/см}^3 \times \left(\pi \frac{(1800 \text{ см})^2}{4} \times 700 \text{ см}\right)\).
Вычислим численное значение массы в граммах:
\(m = 0.85 \times \pi \times \frac{1800^2}{4} \times 700\) г.
\(m = 0.85 \times \pi \times \frac{3240000}{4} \times 700\) г.
\(m = 0.85 \times \pi \times 810000 \times 700\) г.
\(m = 0.85 \times \pi \times 567000000\) г.
Приближенное значение массы составляет \(1514090579\) г.
Для получения ответа в тоннах, необходимо перевести массу из граммов в тонны. \(1\) тонна равна \(1000\) килограммов, а \(1\) килограмм равен \(1000\) граммов, следовательно, \(1\) тонна равна \(1000 \times 1000 = 1000000\) граммов.
Чтобы перевести массу из граммов в тонны, нужно разделить значение в граммах на \(1000000\).
\(m_{\text{тонны}} = \frac{1514090579 \text{ г}}{1000000 \text{ г/т}}\).
\(m = 1514.090579\) т.
Округляя до двух знаков после запятой, получаем \(1514.09\) т.
Ответ: масса нефти составляет \(1514,09\) т.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!