ГДЗ по Геометрии 11 класс Номер 460 Атанасян — Подробные Ответы

Алюминиевый провод диаметром 4 мм имеет массу 6,8 кг. Найдите длину провода (плотность алюминия 2,6 г/см\(^3\)).

Дано: масса провода \(m = 6.8\) кг, диаметр провода \(d = 4\) мм, плотность алюминия \(\rho = 2.6\) г/см\(^3\). Найти: длина провода \(l\).

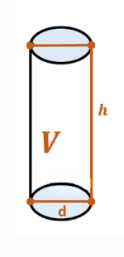
Провод имеет форму цилиндра. Масса провода находится по формуле \(m = V \cdot \rho\), где \(V\) — объем провода, \(\rho\) — плотность. Объем цилиндра равен произведению площади основания на высоту (длину провода): \(V = S_{осн} \cdot l\). Площадь основания круга равна \(S_{осн} = \frac{\pi d^2}{4}\). Подставляя выражения для объема и площади основания в формулу для массы, получаем \(m = \frac{\pi d^2}{4} \cdot l \cdot \rho\). Выразим из этой формулы длину провода: \(l = \frac{4m}{\pi d^2 \rho}\).
Переведем данные в согласованные единицы. Масса \(m = 6.8\) кг = \(6800\) г. Диаметр \(d = 4\) мм = \(0.4\) см. Плотность \(\rho = 2.6\) г/см\(^3\).
Подставим значения в формулу для длины: \(l = \frac{4 \cdot 6800}{\pi \cdot (0.4)^2 \cdot 2.6}\) см.
Вычисляем: \(l = \frac{27200}{\pi \cdot 0.16 \cdot 2.6} = \frac{27200}{\pi \cdot 0.416}\) см. Приближенно \(l \approx \frac{27200}{1.3069} \approx 20813\) см.
Переведем длину в метры: \(20813\) см = \(208.13\) м.
Ответ: длина провода равна \(20813\) см или \(208.13\) м.

Дано:
масса провода \(m = 6.8\) кг
диаметр провода \(d = 4\) мм
плотность алюминия \(\rho = 2.6\) г/см\(^3\)

Найти:
длина провода \(l\)

Решение:
Провод имеет форму цилиндра.
Масса тела связана с его объемом и плотностью формулой:
\(m = V \cdot \rho\)
где \(m\) — масса, \(V\) — объем, \(\rho\) — плотность.

Объем цилиндра вычисляется как произведение площади основания на его высоту (в данном случае, длину провода):
\(V = S_{осн} \cdot l\)
где \(S_{осн}\) — площадь основания, \(l\) — длина провода.

Основание цилиндра представляет собой круг. Площадь круга находится по формуле:
\(S_{осн} = \frac{\pi r^2}{}\) или через диаметр \(d\), где \(r = \frac{d}{2}\):
\(S_{осн} = \pi \left(\frac{d}{2}\right)^2 = \pi \frac{d^2}{4}\)

Теперь подставим выражение для площади основания в формулу для объема цилиндра:
\(V = \frac{\pi d^2}{4} \cdot l\)

Далее подставим выражение для объема в формулу для массы:
\(m = \left(\frac{\pi d^2}{4} \cdot l\right) \cdot \rho\)

Нам нужно найти длину провода \(l\). Выразим \(l\) из полученной формулы:
\(m = \frac{\pi d^2 l \rho}{4}\)
Умножим обе части на 4:
\(4m = \pi d^2 l \rho\)
Разделим обе части на \(\pi d^2 \rho\):
\(l = \frac{4m}{\pi d^2 \rho}\)

Прежде чем проводить вычисления, необходимо убедиться, что все величины выражены в согласованных единицах измерения. В данном случае удобно использовать граммы и сантиметры, так как плотность дана в г/см\(^3\).
Масса дана в килограммах: \(m = 6.8\) кг. Переведем в граммы, зная, что в 1 кг = 1000 г:
\(m = 6.8 \cdot 1000\) г = \(6800\) г.

Диаметр дан в миллиметрах: \(d = 4\) мм. Переведем в сантиметры, зная, что в 1 см = 10 мм:
\(d = \frac{4}{10}\) см = \(0.4\) см.

Плотность уже дана в г/см\(^3\): \(\rho = 2.6\) г/см\(^3\).

Теперь подставим значения всех величин в формулу для длины провода:
\(l = \frac{4 \cdot 6800}{\pi \cdot (0.4)^2 \cdot 2.6}\)

Выполним вычисления шаг за шагом.
Возведем диаметр в квадрат: \((0.4)^2 = 0.4 \cdot 0.4 = 0.16\).
Умножим \(\pi\) на квадрат диаметра и плотность: \(\pi \cdot 0.16 \cdot 2.6\).
Приближенное значение \(\pi \approx 3.14159\).
\(\pi \cdot 0.16 \cdot 2.6 \approx 3.14159 \cdot 0.416 \approx 1.30693\).
Числитель: \(4 \cdot 6800 = 27200\).
Теперь разделим числитель на знаменатель:
\(l = \frac{27200}{\pi \cdot 0.16 \cdot 2.6} = \frac{27200}{0.416\pi}\)
Используя приближенное значение знаменателя:
\(l \approx \frac{27200}{1.30693} \approx 20812.9\) см.
Округлим до целого числа, как в примере: \(l \approx 20813\) см.

Длина провода в сантиметрах составляет \(20813\) см.
Переведем эту длину в метры, зная, что в 1 м = 100 см:
\(l = \frac{20813}{100}\) м = \(208.13\) м.

Ответ: длина провода составляет \(20813\) см, что равно \(208.13\) м.