ГДЗ по Геометрии 11 класс Номер 457 Атанасян — Подробные Ответы

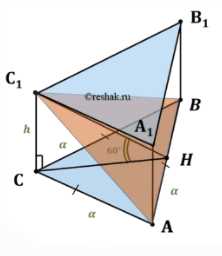
В правильной треугольной призме через сторону нижнего основания и противолежащую ей вершину верхнего основания проведено сечение, составляющее угол в 60° с плоскостью основания. Найдите объём призмы, если сторона основания равна \(a\).

Объем призмы равен произведению площади основания на высоту: \(V_{\text{призмы}} = S_{\text{основания}} \cdot h\). Основание является равносторонним треугольником со стороной \(a\), поэтому его площадь \(S_{\text{основания}} = \frac{\sqrt{3}}{4} a^2\). Высота основания \(CH = \frac{\sqrt{3}}{2} a\). В прямоугольном треугольнике \(C_1HC\) высота призмы \(h = C_1C = CH \cdot \tan(60^\circ) = \frac{\sqrt{3}}{2} a \cdot \sqrt{3} = \frac{3a}{2}\). Таким образом, объем призмы \(V_{\text{призмы}} = \frac{\sqrt{3}}{4} a^2 \cdot \frac{3a}{2} = \frac{3\sqrt{3}a^3}{8}\). Ответ: \(V_{\text{призмы}} = \frac{3\sqrt{3}a^3}{8}\).

Дано: правильная призма \(ABCA_1B_1C_1\), сторона основания \(AB = BC = CA = a\), угол между сечением \(ABC_1\) и плоскостью основания \(ABC\) равен \(60^\circ\). Найти: объем призмы \(V_{\text{призмы}}\).

Объем призмы находится по формуле \(V_{\text{призмы}} = S_{\text{основания}} \cdot h\), где \(S_{\text{основания}}\) — площадь основания, а \(h\) — высота призмы.

Основанием правильной призмы является правильный многоугольник. В данном случае, основание — равносторонний треугольник \(ABC\) со стороной \(a\). Площадь равностороннего треугольника со стороной \(a\) вычисляется по формуле \(S = \frac{\sqrt{3}}{4} a^2\). Следовательно, площадь основания \(S_{\text{основания}} = \frac{\sqrt{3}}{4} a^2\).

Чтобы найти высоту призмы \(h = C_1C\), рассмотрим сечение \(ABC_1\). Угол между плоскостью сечения \(ABC_1\) и плоскостью основания \(ABC\) равен \(60^\circ\). Линейным углом двугранного угла между плоскостями \(ABC_1\) и \(ABC\) является угол между перпендикулярами к линии пересечения этих плоскостей, проведенными в каждой из плоскостей. Линией пересечения является сторона \(AB\).

Проведем медиану \(CH\) в треугольнике \(ABC\) к стороне \(AB\). Так как треугольник \(ABC\) равносторонний, \(CH\) также является высотой и биссектрисой. \(CH \perp AB\). Длина высоты равностороннего треугольника со стороной \(a\) равна \(CH = \frac{\sqrt{3}}{2} a\).

В треугольнике \(ABC_1\), \(C_1H\) является медианой к стороне \(AB\), так как \(H\) — середина \(AB\), а \(C_1A = C_1B\) (как диагонали равных боковых граней \(ACC_1A_1\) и \(BCC_1B_1\), которые являются прямоугольниками с одинаковыми сторонами \(a\) и \(h\)). В равнобедренном треугольнике \(ABC_1\), медиана \(C_1H\) является также высотой, то есть \(C_1H \perp AB\).

Таким образом, угол \(∠C_1HC\) является линейным углом двугранного угла между плоскостями \(ABC_1\) и \(ABC\), и по условию он равен \(60^\circ\).

Рассмотрим прямоугольный треугольник \(C_1HC\). Катет \(CH = \frac{\sqrt{3}}{2} a\), угол \(∠C_1HC = 60^\circ\), а катет \(C_1C\) является высотой призмы \(h\). В прямоугольном треугольнике тангенс угла равен отношению противолежащего катета к прилежащему. Следовательно, \(C_1C = CH \cdot \tan(∠C_1HC)\).

Подставляя значения, получаем \(h = \frac{\sqrt{3}}{2} a \cdot \tan(60^\circ) = \frac{\sqrt{3}}{2} a \cdot \sqrt{3} = \frac{3a}{2}\).

Теперь подставим значения площади основания и высоты в формулу объема призмы: \(V_{\text{призмы}} = S_{\text{основания}} \cdot h = \frac{\sqrt{3}}{4} a^2 \cdot \frac{3a}{2}\).

Выполним умножение: \(V_{\text{призмы}} = \frac{\sqrt{3} \cdot 3 \cdot a^2 \cdot a}{4 \cdot 2} = \frac{3\sqrt{3}a^3}{8}\).

Таким образом, объем призмы равен \(\frac{3\sqrt{3}a^3}{8}\).

Ответ: \(V_{\text{призмы}} = \frac{3\sqrt{3}a^3}{8}\).