
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 456 Атанасян — Подробные Ответы
Найдите объём правильной \(n\)-угольной призмы, у которой каждое ребро равно \(a\), если: а) \(n = 3\); б) \(n = 4\); в) \(n = 6\); г) \(n = 8\)
Объем правильной \(n\)-угольной призмы с ребром \(a\) находится по формуле \(V = S_{осн} \cdot h\). Поскольку все ребра равны \(a\), высота призмы \(h=a\). Площадь основания \(S_{осн}\) правильного \(n\)-угольника равна \(n\) умножить на площадь треугольника с вершинами в центре многоугольника и на концах одной стороны: \(S_{осн} = n \cdot \frac{a^2}{4} \text{ctg}\left(\frac{180^\circ}{n}\right)\). Тогда объем призмы \(V_n = \frac{a^3 n}{4} \text{ctg}\left(\frac{180^\circ}{n}\right)\).
а) При \(n=3\): \(V_3 = \frac{a^3 \cdot 3}{4} \text{ctg}\left(\frac{180^\circ}{3}\right) = \frac{3a^3}{4} \text{ctg}(60^\circ) = \frac{3a^3}{4} \cdot \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{4}a^3\).
б) При \(n=4\): \(V_4 = \frac{a^3 \cdot 4}{4} \text{ctg}\left(\frac{180^\circ}{4}\right) = a^3 \text{ctg}(45^\circ) = a^3 \cdot 1 = a^3\).
в) При \(n=6\): \(V_6 = \frac{a^3 \cdot 6}{4} \text{ctg}\left(\frac{180^\circ}{6}\right) = \frac{3a^3}{2} \text{ctg}(30^\circ) = \frac{3a^3}{2} \cdot \sqrt{3} = \frac{3\sqrt{3}}{2}a^3\).
г) При \(n=8\): \(V_8 = \frac{a^3 \cdot 8}{4} \text{ctg}\left(\frac{180^\circ}{8}\right) = 2a^3 \text{ctg}(22.5^\circ)\). Поскольку \(\text{ctg}(22.5^\circ) = \sqrt{2}+1\), \(V_8 = 2a^3 (\sqrt{2}+1)\).
Ответ: \(V_{n=3} = \frac{\sqrt{3}}{4}a^3, V_{n=4} = a^3, V_{n=6} = \frac{3\sqrt{3}}{2} a^3, V_{n=8} = 2 (\sqrt{2} + 1) a^3\).
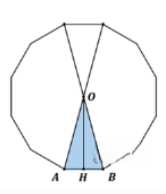
Объем призмы равен произведению площади основания на высоту. В данном случае призма правильная \(n\)-угольная, и все ее ребра равны \(a\), следовательно, высота призмы \(h = a\). Основанием является правильный \(n\)-угольник со стороной \(a\). Площадь правильного \(n\)-угольника можно найти, разбив его на \(n\) равных равнобедренных треугольников с общей вершиной в центре многоугольника. Рассмотрим один такой треугольник \(AOB\), где \(O\) — центр многоугольника, а \(AB\) — одна из сторон длиной \(a\). Угол при вершине \(O\) равен \(\frac{360^\circ}{n}\). Опустим высоту \(OH\) из \(O\) на сторону \(AB\). Эта высота является апофемой многоугольника и делит угол \(\angle AOB\) и сторону \(AB\) пополам. В прямоугольном треугольнике \(AHO\), угол \(\angle AOH = \frac{1}{2} \cdot \frac{360^\circ}{n} = \frac{180^\circ}{n}\), а катет \(AH = \frac{a}{2}\). Апофема \(OH\) связана с \(AH\) и углом \(\angle AOH\) соотношением \(OH = AH \cdot \text{ctg}(\angle AOH) = \frac{a}{2} \text{ctg}\left(\frac{180^\circ}{n}\right)\). Площадь треугольника \(AOB\) равна половине произведения основания на высоту: \(S_{\triangle AOB} = \frac{1}{2} \cdot AB \cdot OH = \frac{1}{2} \cdot a \cdot \frac{a}{2} \text{ctg}\left(\frac{180^\circ}{n}\right) = \frac{a^2}{4} \text{ctg}\left(\frac{180^\circ}{n}\right)\). Площадь основания \(S_{осн}\) правильного \(n\)-угольника равна \(n\) умножить на площадь одного такого треугольника: \(S_{осн} = n \cdot S_{\triangle AOB} = n \cdot \frac{a^2}{4} \text{ctg}\left(\frac{180^\circ}{n}\right) = \frac{na^2}{4} \text{ctg}\left(\frac{180^\circ}{n}\right)\). Объем призмы \(V_n\) равен произведению площади основания на высоту: \(V_n = S_{осн} \cdot h = \frac{na^2}{4} \text{ctg}\left(\frac{180^\circ}{n}\right) \cdot a = \frac{na^3}{4} \text{ctg}\left(\frac{180^\circ}{n}\right)\).
Теперь подставим заданные значения \(n\):
а) Для \(n=3\) (правильная треугольная призма): Угол \(\frac{180^\circ}{3} = 60^\circ\). \(\text{ctg}(60^\circ) = \frac{1}{\sqrt{3}}\).
\(V_3 = \frac{3a^3}{4} \text{ctg}(60^\circ) = \frac{3a^3}{4} \cdot \frac{1}{\sqrt{3}} = \frac{3a^3 \cdot \sqrt{3}}{4 \cdot \sqrt{3} \cdot \sqrt{3}} = \frac{3a^3 \sqrt{3}}{4 \cdot 3} = \frac{\sqrt{3}}{4}a^3\).
б) Для \(n=4\) (правильная четырехугольная призма, т.е. куб, так как все ребра равны \(a\)): Угол \(\frac{180^\circ}{4} = 45^\circ\). \(\text{ctg}(45^\circ) = 1\).
\(V_4 = \frac{4a^3}{4} \text{ctg}(45^\circ) = a^3 \cdot 1 = a^3\).
в) Для \(n=6\) (правильная шестиугольная призма): Угол \(\frac{180^\circ}{6} = 30^\circ\). \(\text{ctg}(30^\circ) = \sqrt{3}\).
\(V_6 = \frac{6a^3}{4} \text{ctg}(30^\circ) = \frac{3a^3}{2} \cdot \sqrt{3} = \frac{3\sqrt{3}}{2}a^3\).
г) Для \(n=8\) (правильная восьмиугольная призма): Угол \(\frac{180^\circ}{8} = 22.5^\circ\). Найдем \(\text{ctg}(22.5^\circ)\) используя формулу половинного угла \(\text{ctg}\left(\frac{\alpha}{2}\right) = \frac{\sin(\alpha)}{1 — \cos(\alpha)}\) при \(\alpha = 45^\circ\).
\(\text{ctg}(22.5^\circ) = \frac{\sin(45^\circ)}{1 — \cos(45^\circ)} = \frac{\frac{\sqrt{2}}{2}}{1 — \frac{\sqrt{2}}{2}} = \frac{\sqrt{2}}{2 — \sqrt{2}}\). Домножим числитель и знаменатель на сопряженное выражение \(2 + \sqrt{2}\): \(\frac{\sqrt{2}(2 + \sqrt{2})}{(2 — \sqrt{2})(2 + \sqrt{2})} = \frac{2\sqrt{2} + (\sqrt{2})^2}{2^2 — (\sqrt{2})^2} = \frac{2\sqrt{2} + 2}{4 — 2} = \frac{2\sqrt{2} + 2}{2} = \sqrt{2} + 1\).
\(V_8 = \frac{8a^3}{4} \text{ctg}(22.5^\circ) = 2a^3 (\sqrt{2} + 1)\).
Таким образом, объемы призмы для заданных \(n\) равны: \(V_{n=3} = \frac{\sqrt{3}}{4}a^3\), \(V_{n=4} = a^3\), \(V_{n=6} = \frac{3\sqrt{3}}{2} a^3\), \(V_{n=8} = 2 (\sqrt{2} + 1) a^3\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!