Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 455 Атанасян — Подробные Ответы
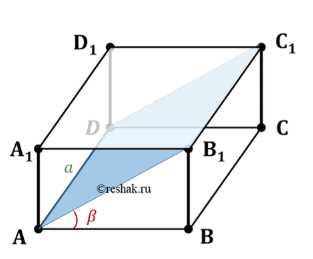
Основанием прямой призмы является параллелограмм. Через сторону основания, равную \(a\), и противолежащую ей сторону другого основания проведено сечение, составляющее угол \(\beta\) с плоскостью основания. Площадь сечения равна \(Q\). Найдите объём призмы.
Объем призмы равен произведению площади основания на высоту. Площадь основания параллелограмма ABCD равна \(S_{ABCD} = AD \cdot h_{ABCD}\), где \(h_{ABCD}\) — высота параллелограмма, опущенная на сторону AD. Площадь сечения ADC₁B₁ равна \(S_{ADC₁B₁} = AD \cdot h_{ADC₁B₁} = Q\), где \(h_{ADC₁B₁}\) — высота параллелограмма ADC₁B₁, опущенная на сторону AD. Из прямоугольного треугольника, образованного высотой призмы \(h\), \(h_{ABCD}\) и \(h_{ADC₁B₁}\), угол между \(h_{ABCD}\) и \(h_{ADC₁B₁}\) равен \(\beta\). Следовательно, \(h_{ABCD} = h_{ADC₁B₁} \cos(\beta)\) и \(h = h_{ADC₁B₁} \sin(\beta)\). Из \(a \cdot h_{ADC₁B₁} = Q\) находим \(h_{ADC₁B₁} = \frac{Q}{a}\). Тогда \(h_{ABCD} = \frac{Q}{a} \cos(\beta)\) и \(h = \frac{Q}{a} \sin(\beta)\). Площадь основания \(S_{ABCD} = a \cdot h_{ABCD} = a \cdot \frac{Q}{a} \cos(\beta) = Q \cos(\beta)\). Объем призмы \(V_{призмы} = S_{ABCD} \cdot h = (Q \cos(\beta)) \cdot (\frac{Q}{a} \sin(\beta)) = \frac{Q^2 \cos(\beta) \sin(\beta)}{a}\).
Дано: прямая призма \(ABCDA₁B₁C₁D₁\), основание \(ABCD\) — параллелограмм, \(AD = a\), \(\angle B₁ADC = \beta\), площадь сечения \(ADC₁B₁\) равна \(Q\). Найти объем призмы \(V_{призмы}\).
Объем прямой призмы равен произведению площади основания на высоту призмы: \(V_{призмы} = S_{основания} \cdot h\).
Основанием призмы является параллелограмм \(ABCD\). Площадь параллелограмма \(ABCD\) может быть найдена как произведение стороны на высоту, опущенную на эту сторону. Возьмем сторону \(AD\), тогда \(S_{ABCD} = AD \cdot h_{ABCD}\), где \(h_{ABCD}\) — высота параллелограмма \(ABCD\), проведенная к стороне \(AD\).
Сечение \(ADC₁B₁\) проходит через сторону основания \(AD\) и противолежащую ей сторону верхнего основания \(B₁C₁\). Поскольку \(ABCD\) — параллелограмм, \(BC \parallel AD\) и \(BC = AD\). В прямой призме боковые ребра перпендикулярны основаниям, и \(B₁C₁\) параллельна и равна \(BC\). Следовательно, \(B₁C₁ \parallel AD\) и \(B₁C₁ = AD\). Четырехугольник \(ADC₁B₁\) имеет две параллельные и равные стороны \(AD\) и \(B₁C₁\), поэтому он является параллелограммом.
Площадь сечения \(ADC₁B₁\) равна \(Q\). Площадь параллелограмма \(ADC₁B₁\) может быть найдена как произведение стороны \(AD\) на высоту \(h_{ADC₁B₁}\), проведенную к этой стороне: \(S_{ADC₁B₁} = AD \cdot h_{ADC₁B₁} = Q\). Отсюда можно выразить высоту \(h_{ADC₁B₁}\): \(h_{ADC₁B₁} = \frac{Q}{AD} = \frac{Q}{a}\).
Высота \(h_{ABCD}\) параллелограмма \(ABCD\), проведенная к \(AD\), и высота \(h_{ADC₁B₁}\) параллелограмма \(ADC₁B₁\), проведенная к \(AD\), лежат в плоскостях, перпендикулярных \(AD\). Угол между этими высотами равен углу между плоскостью основания \(ABCD\) и плоскостью сечения \(ADC₁B₁\), который по условию равен \(\beta\). Высота призмы \(h\) — это расстояние между плоскостями оснований, она перпендикулярна обеим плоскостям. Рассмотрим прямоугольный треугольник, образованный высотой призмы \(h\), высотой \(h_{ABCD}\) и высотой \(h_{ADC₁B₁}\). В этом треугольнике \(h_{ADC₁B₁}\) является гипотенузой, а \(h_{ABCD}\) и \(h\) — катетами. Угол \(\beta\) является углом между \(h_{ABCD}\) и \(h_{ADC₁B₁}\).
Из этого прямоугольного треугольника имеем:
\(h_{ABCD} = h_{ADC₁B₁} \cos(\beta)\)
\(h = h_{ADC₁B₁} \sin(\beta)\)
Подставим значение \(h_{ADC₁B₁} = \frac{Q}{a}\) в эти уравнения:
\(h_{ABCD} = \frac{Q}{a} \cos(\beta)\)
\(h = \frac{Q}{a} \sin(\beta)\)
Теперь найдем площадь основания \(S_{ABCD}\):
\(S_{ABCD} = AD \cdot h_{ABCD} = a \cdot \left(\frac{Q}{a} \cos(\beta)\right) = Q \cos(\beta)\).
Наконец, вычислим объем призмы \(V_{призмы}\):
\(V_{призмы} = S_{основания} \cdot h = S_{ABCD} \cdot h = (Q \cos(\beta)) \cdot \left(\frac{Q}{a} \sin(\beta)\right) = \frac{Q^2 \cos(\beta) \sin(\beta)}{a}\).
Таким образом, объем призмы равен \(\frac{Q^2 \cos(\beta) \sin(\beta)}{a}\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.