
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 453 Атанасян — Подробные Ответы
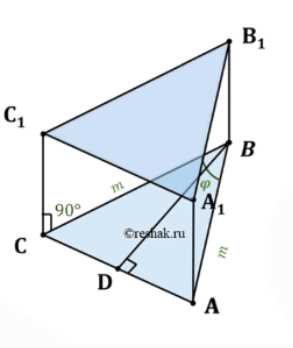
Найдите объём прямой призмы \(ARCA_1B_1C_1\), если \(AR = RC = m\), \(\angle ABC = \phi\) и \(ВB_1 = BD\), где \(BD\) — высота треугольника АВС.
Решение:
Объем прямой призмы равен произведению площади основания на высоту: \(V_{призмы} = S_{основания} \cdot h\).
Основанием является треугольник ABC. Так как \(AB = BC = m\) и \(\angle ABC = \phi\), а BD — высота, проведенная к AC, то в равнобедренном треугольнике ABD имеем \(AD = AB \sin(\frac{\phi}{2}) = m \sin(\frac{\phi}{2})\) и \(BD = AB \cos(\frac{\phi}{2}) = m \cos(\frac{\phi}{2})\).
Поскольку BD является также медианой, \(AC = 2 \cdot AD = 2m \sin(\frac{\phi}{2})\).
Площадь основания \(S_{основания} = \frac{1}{2} \cdot AC \cdot BD = \frac{1}{2} \cdot (2m \sin(\frac{\phi}{2})) \cdot (m \cos(\frac{\phi}{2})) = m^2 \sin(\frac{\phi}{2}) \cos(\frac{\phi}{2})\).
Высота призмы равна \(h = BB_1 = BD = m \cos(\frac{\phi}{2})\).
Следовательно, объем призмы \(V_{призмы} = S_{основания} \cdot h = (m^2 \sin(\frac{\phi}{2}) \cos(\frac{\phi}{2})) \cdot (m \cos(\frac{\phi}{2})) = \)
\(=m^3 \sin(\frac{\phi}{2}) \cos^2(\frac{\phi}{2})\).
Ответ: \(V_{призмы} = m^3 \sin(\frac{\phi}{2}) \cos^2(\frac{\phi}{2})\).
Дано: прямая призма \(ABCA_1B_1C_1\), \(\angle ABC = \phi\), \(AB = BC = m\), \(BD \perp AC\), \(BB_1 = BD\).
Найти: Объем призмы \(V_{призмы}\).
Решение:
Объем прямой призмы определяется формулой \(V_{призмы} = S_{основания} \cdot h\), где \(S_{основания}\) — площадь основания, а \(h\) — высота призмы.
В данном случае основанием является треугольник ABC, а высота призмы — отрезок \(BB_1\).
Рассмотрим треугольник ABC. Из условия дано, что \(AB = BC = m\), следовательно, треугольник ABC является равнобедренным с основанием AC.
Отрезок BD является высотой, проведенной из вершины B к основанию AC (\(BD \perp AC\)). В равнобедренном треугольнике высота, проведенная к основанию, одновременно является биссектрисой угла при вершине B и медианой к основанию AC.
Рассмотрим прямоугольный треугольник ABD (угол ADB прямой, так как BD — высота). В этом треугольнике гипотенуза \(AB = m\), а угол ABD равен половине угла ABC, то есть \(\angle ABD = \frac{\angle ABC}{2} = \frac{\phi}{2}\).
Используя тригонометрические соотношения в прямоугольном треугольнике ABD, найдем длины отрезков AD и BD.
Катет AD, противолежащий углу \(\frac{\phi}{2}\), равен \(AD = AB \cdot \sin(\angle ABD) = m \sin(\frac{\phi}{2})\).
Катет BD, прилежащий к углу \(\frac{\phi}{2}\), равен \(BD = AB \cdot \cos(\angle ABD) = m \cos(\frac{\phi}{2})\).
Так как BD является медианой в равнобедренном треугольнике ABC, точка D является серединой отрезка AC. Следовательно, длина основания AC равна удвоенной длине отрезка AD: \(AC = 2 \cdot AD = 2 \cdot (m \sin(\frac{\phi}{2})) = 2m \sin(\frac{\phi}{2})\).
Теперь найдем площадь основания — треугольника ABC. Площадь треугольника можно вычислить по формуле \(S = \frac{1}{2} \cdot основание \cdot высота\). В качестве основания возьмем AC, а в качестве высоты — BD.
\(S_{основания} = S_{ABC} = \frac{1}{2} \cdot AC \cdot BD = \frac{1}{2} \cdot (2m \sin(\frac{\phi}{2})) \cdot (m \cos(\frac{\phi}{2}))\).
Упрощая выражение для площади основания, получаем \(S_{основания} = m^2 \sin(\frac{\phi}{2}) \cos(\frac{\phi}{2})\).
Высота призмы \(h\) равна длине отрезка \(BB_1\). Из условия дано, что \(BB_1 = BD\).
Мы уже нашли длину отрезка BD: \(BD = m \cos(\frac{\phi}{2})\).
Следовательно, высота призмы \(h = BB_1 = m \cos(\frac{\phi}{2})\).
Теперь можем вычислить объем призмы, используя найденные значения площади основания и высоты:
\(V_{призмы} = S_{основания} \cdot h = (m^2 \sin(\frac{\phi}{2}) \cos(\frac{\phi}{2})) \cdot (m \cos(\frac{\phi}{2}))\).
Умножая эти выражения, получаем окончательную формулу для объема призмы:
\(V_{призмы} = m^{2+1} \sin(\frac{\phi}{2}) \cos^{1+1}(\frac{\phi}{2}) = m^3 \sin(\frac{\phi}{2}) \cos^2(\frac{\phi}{2})\).
Таким образом, объем прямой призмы \(ABCA_1B_1C_1\) равен \(m^3 \sin(\frac{\phi}{2}) \cos^2(\frac{\phi}{2})\).
Ответ: Объем призмы \(V_{призмы} = m^3 \sin(\frac{\phi}{2}) \cos^2(\frac{\phi}{2})\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!