
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 452 Атанасян — Подробные Ответы
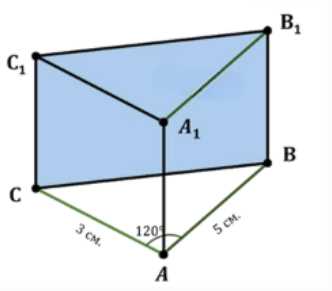
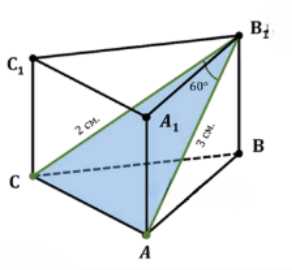
Найдите объём прямой призмы \(ABCA_1B_1C_1\), если: а) \(\angle ВАС = 120°\), \(АВ = 5\) см, \(АС = 3\) см и наибольшая из площадей боковых граней равна 35 см\(^2\); б) \(\angle ABC = 60°\), \(АВ_1 = 3\), \(СВ_1 = 2\) и двугранный угол с ребром \(ВВ_1\) прямой.
а) По теореме косинусов из \( \triangle ABC \): \( BC^2 = AB^2 + AC^2 — 2 \cdot AB \cdot AC \cdot \cos(\angle BAC) \). Подставляя значения, получаем \( BC^2 = 5^2 + 3^2 — 2 \cdot 5 \cdot 3 \cdot (-\frac{1}{2}) = 25 + 9 + 15 = 49 \), откуда \( BC = 7 \) см. Наибольшая боковая грань \( BCC_1B_1 \) имеет площадь \( S_{BCC_1B_1} = BC \cdot h = 35 \), где \( h \) — высота призмы. Отсюда \( 7 \cdot h = 35 \), значит \( h = 5 \) см.
Площадь основания \( S_{ABC} = \frac{1}{2} \cdot AB \cdot AC \cdot \sin(\angle BAC) = \frac{1}{2} \cdot 5 \cdot 3 \cdot \sin(120^\circ) = \frac{1}{2} \cdot 15 \cdot \frac{\sqrt{3}}{2} = \)
\(=\frac{15\sqrt{3}}{4} \) см\(^2\).
Объем призмы \( V = S_{ABC} \cdot h = \frac{15\sqrt{3}}{4} \cdot 5 = \frac{75\sqrt{3}}{4} \) см\(^3\).
б) Из условия, что двугранный угол с ребром \( BB_1 \) прямой, следует, что \( \angle ABC = 90^\circ \). Рассмотрим прямоугольные треугольники \( \triangle ABC \), \( \triangle ABB_1 \) и \( \triangle CBB_1 \). По теореме Пифагора: \( AB^2 + BC^2 = AC^2 \), \( AB^2 + BB_1^2 = AB_1^2 = 3^2 = 9 \), \( BC^2 + BB_1^2 = CB_1^2 = 2^2 = 4 \). Из первого изображения задачи б) по теореме косинусов из \( \triangle AB_1C \) найдено \( AC^2 = AB_1^2 + B_1C^2 — 2 \cdot AB_1 \cdot B_1C \cdot \cos(\angle AB_1C) = 3^2 +\)
\(+ 2^2 — 2 \cdot 3 \cdot 2 \cdot \cos(60^\circ) = 9 + 4 — 12 \cdot \frac{1}{2} = 13 — 6 = 7 \), следовательно \( AC = \sqrt{7} \). Таким образом, имеем систему уравнений: \( AB^2 + BC^2 = 7 \), \( AB^2 + BB_1^2 = 9 \), \( BC^2 + BB_1^2 = 4 \). Вычитая третье уравнение из первого, получаем \( AB^2 — BB_1^2 = 3 \). Складывая это с третьим уравнением, получаем \( AB^2 + BC^2 = 7 \). Из второго и третьего уравнений: \( AB^2 — BC^2 = 9 — 4 = 5 \). Складывая \( AB^2 + BC^2 = 7 \) и \( AB^2 — BC^2 = 5 \), получаем \( 2AB^2 = 12 \), откуда \( AB^2 = 6 \) и \( AB = \sqrt{6} \) см. Подставляя \( AB^2 = 6 \) в \( AB^2 + BC^2 = 7 \), получаем \( 6 + BC^2 = 7 \), откуда \( BC^2 = 1 \) и \( BC = 1 \) см. Подставляя \( BC^2 = 1 \) в \( BC^2 + BB_1^2 = 4 \), получаем \( 1 + BB_1^2 = 4 \), откуда \( BB_1^2 = 3 \) и \( BB_1 = \sqrt{3} \) см. Площадь основания \( S_{ABC} = \frac{1}{2} \cdot AB \cdot BC = \frac{1}{2} \cdot \sqrt{6} \cdot 1 = \frac{\sqrt{6}}{2} \) см\(^2\). Высота призмы \( h = BB_1 = \sqrt{3} \) см. Объем призмы \( V = S_{ABC} \cdot h = \frac{\sqrt{6}}{2} \cdot \sqrt{3} = \frac{\sqrt{18}}{2} = \frac{3\sqrt{2}}{2} \) см\(^3\).
а) Для нахождения объема прямой призмы необходимо найти площадь основания и высоту призмы. Основанием является треугольник \( ABC \). Известны две стороны \( AB = 5 \) см, \( AC = 3 \) см и угол между ними \( \angle BAC = 120^\circ \). Третью сторону основания \( BC \) можно найти по теореме косинусов: \( BC^2 = AB^2 + AC^2 — 2 \cdot AB \cdot AC \cdot \cos(\angle BAC) \). Подставляя данные, получаем \( BC^2 = 5^2 + 3^2 — 2 \cdot 5 \cdot 3 \cdot \cos(120^\circ) \). Поскольку \( \cos(120^\circ) = -\frac{1}{2} \), имеем \( BC^2 = 25 + 9 — 30 \cdot (-\frac{1}{2}) = 34 + 15 = 49 \). Следовательно, \( BC = \sqrt{49} = 7 \) см.
Площади боковых граней прямой призмы равны произведению стороны основания на высоту призмы. Стороны основания равны 5 см, 3 см, и 7 см. Наибольшей боковой гранью будет та, у которой сторона основания наибольшая. В данном случае это грань \( BCC_1B_1 \), так как \( BC = 7 \) см является наибольшей стороной треугольника \( ABC \). Площадь этой грани равна 35 см\(^2\). Обозначим высоту призмы через \( h \). Тогда \( S_{BCC_1B_1} = BC \cdot h \). Подставляя известные значения, получаем \( 7 \cdot h = 35 \), откуда \( h = \frac{35}{7} = 5 \) см.
Площадь основания \( S_{ABC} \) можно найти по формуле \( S_{ABC} = \frac{1}{2} \cdot AB \cdot AC \cdot \sin(\angle BAC) \). Подставляем значения: \( S_{ABC} = \frac{1}{2} \cdot 5 \cdot 3 \cdot \sin(120^\circ) \). Поскольку \( \sin(120^\circ) = \sin(180^\circ — 60^\circ) = \sin(60^\circ) = \frac{\sqrt{3}}{2} \), имеем \( S_{ABC} = \frac{1}{2} \cdot 15 \cdot \frac{\sqrt{3}}{2} = \frac{15\sqrt{3}}{4} \) см\(^2\).
Объем прямой призмы равен произведению площади основания на высоту: \( V_{ABCA_1B_1C_1} = S_{ABC} \cdot h \). Подставляем найденные значения: \( V_{ABCA_1B_1C_1} = \frac{15\sqrt{3}}{4} \cdot 5 = \frac{75\sqrt{3}}{4} \) см\(^3\).
б) В данной прямой призме двугранный угол с ребром \( BB_1 \) прямой. Поскольку призма прямая, ребро \( BB_1 \) перпендикулярно плоскости основания \( ABC \). Двугранный угол с ребром \( BB_1 \) — это угол между плоскостями, проходящими через \( BB_1 \). Если этот угол прямой, это означает, что плоскости, содержащие боковые грани, перпендикулярны друг другу вдоль ребра \( BB_1 \). В контексте прямой призмы, это условие обычно указывает на то, что угол между сторонами основания, сходящимися в вершине, из которой выходит ребро \( BB_1 \), является прямым. Таким образом, \( \angle ABC = 90^\circ \).
Рассмотрим треугольник \( AB_1C \). По теореме косинусов в \( \triangle AB_1C \): \( AC^2 = AB_1^2 + B_1C^2 — 2 \cdot AB_1 \cdot B_1C \cdot \cos(\angle AB_1C) \). Из дано \( AB_1 = 3 \), \( CB_1 = 2 \), \( \angle AB_1C = 60^\circ \). Подставляем: \( AC^2 = 3^2 + 2^2 — 2 \cdot 3 \cdot 2 \cdot \cos(60^\circ) = 9 + 4 — 12 \cdot \frac{1}{2} = 13 — 6 = 7 \). Следовательно, \( AC = \sqrt{7} \).
Теперь рассмотрим прямоугольные треугольники, образованные ребрами призмы. Поскольку \( \angle ABC = 90^\circ \), \( \triangle ABC \) — прямоугольный. По теореме Пифагора в \( \triangle ABC \): \( AB^2 + BC^2 = AC^2 \). В \( \triangle ABB_1 \) (прямоугольный, так как призма прямая): \( AB^2 + BB_1^2 = AB_1^2 \). В \( \triangle CBB_1 \) (прямоугольный): \( BC^2 + BB_1^2 = CB_1^2 \).
Мы имеем систему уравнений:
\( AB^2 + BC^2 = (\sqrt{7})^2 = 7 \)
\( AB^2 + BB_1^2 = 3^2 = 9 \)
\( BC^2 + BB_1^2 = 2^2 = 4 \)
Вычтем третье уравнение из второго: \( (AB^2 + BB_1^2) — (BC^2 + BB_1^2) = 9 — 4 \), что дает \( AB^2 — BC^2 = 5 \).
Теперь у нас есть два уравнения с \( AB^2 \) и \( BC^2 \):
\( AB^2 + BC^2 = 7 \)
\( AB^2 — BC^2 = 5 \)
Сложим эти два уравнения: \( (AB^2 + BC^2) + (AB^2 — BC^2) = 7 + 5 \), что дает \( 2AB^2 = 12 \), откуда \( AB^2 = 6 \) и \( AB = \sqrt{6} \) см.
Подставим \( AB^2 = 6 \) в \( AB^2 + BC^2 = 7 \): \( 6 + BC^2 = 7 \), откуда \( BC^2 = 1 \) и \( BC = 1 \) см.
Подставим \( BC^2 = 1 \) в \( BC^2 + BB_1^2 = 4 \): \( 1 + BB_1^2 = 4 \), откуда \( BB_1^2 = 3 \) и \( BB_1 = \sqrt{3} \) см. Высота призмы \( h = BB_1 = \sqrt{3} \) см.
Площадь основания \( S_{ABC} \) (прямоугольного треугольника) равна \( S_{ABC} = \frac{1}{2} \cdot AB \cdot BC \). Подставляем найденные значения: \( S_{ABC} = \frac{1}{2} \cdot \sqrt{6} \cdot 1 = \frac{\sqrt{6}}{2} \) см\(^2\).
Объем прямой призмы равен произведению площади основания на высоту: \( V_{ABCA_1B_1C_1} = S_{ABC} \cdot h \). Подставляем: \( V_{ABCA_1B_1C_1} = \frac{\sqrt{6}}{2} \cdot \sqrt{3} = \frac{\sqrt{18}}{2} = \frac{3\sqrt{2}}{2} \) см\(^3\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!