
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 451 Атанасян — Подробные Ответы
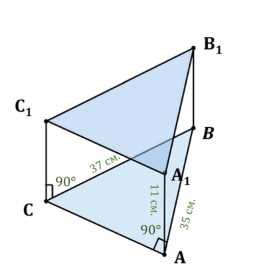
Найдите объём прямой призмы \(ABCA_1B_1C_1\), если \(\angle ВАС = 90°\), \(ВС = 37\) см, \(АВ = 35\) см, \(АА_1 = 1,1\) дм
Дано: прямая призма \(ABCA_1B_1C_1\), \(\angle ВАС = 90°\), \(ВС = 37\) см, \(АВ = 35\) см, \(АА_1 = 1,1\) дм. Найти: \(V_{\text{призмы}}\). Объем прямой призмы равен произведению площади основания на высоту: \(V_{\text{призмы}} = S_{\text{основания}} \cdot h\). Основанием является прямоугольный треугольник \(ABC\). Площадь прямоугольного треугольника равна половине произведения катетов: \(S_{\text{основания}} = \frac{1}{2} \cdot AB \cdot AC\). По теореме Пифагора в \(\triangle ABC\) найдем катет \(AC\): \(BC^2 = AB^2 + AC^2\), откуда \(AC^2 = BC^2 — AB^2 = 37^2 — 35^2 = (37-35)(37+35) = 2 \cdot 72 = 144\). Следовательно, \(AC = \sqrt{144} = 12\) см. Высота призмы \(h = AA_1 = 1,1\) дм \(= 11\) см.
Теперь вычислим площадь основания: \(S_{\text{основания}} = \frac{1}{2} \cdot 35 \cdot 12 = 35 \cdot 6 = 210\) см². Объем призмы: \(V_{\text{призмы}} = S_{\text{основания}} \cdot h = 210 \cdot 11 = 2310\) см³. Ответ: \(V_{\text{призмы}} = 2310\) см³.
Дано: прямая призма \(ABCA_1B_1C_1\). Угол \(\angle ВАС = 90°\). Длина ребра \(ВС = 37\) см. Длина ребра \(АВ = 35\) см. Длина ребра \(АА_1 = 1,1\) дм.
Найти: Объем призмы \(V_{\text{призмы}}\).
Решение:
Объем прямой призмы вычисляется как произведение площади ее основания на высоту. Основанием данной призмы является треугольник \(ABC\), а высотой — ребро \(AA_1\). Формула для объема призмы: \(V_{\text{призмы}} = S_{\text{основания}} \cdot h\), где \(S_{\text{основания}}\) — площадь основания, \(h\) — высота призмы.
Основание призмы — прямоугольный треугольник \(ABC\), так как задан угол \(\angle ВАС = 90°\). Площадь прямоугольного треугольника равна половине произведения длин его катетов. В данном треугольнике катетами являются стороны \(AB\) и \(AC\), а гипотенузой — сторона \(BC\). Формула для площади основания: \(S_{\text{основания}} = \frac{1}{2} \cdot AB \cdot AC\).
Чтобы найти площадь основания, нам необходимо знать длины катетов \(AB\) и \(AC\). Длина катета \(AB\) дана и равна \(35\) см. Длину катета \(AC\) найдем, используя теорему Пифагора в прямоугольном треугольнике \(ABC\). Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. В нашем случае гипотенуза — \(BC\), а катеты — \(AB\) и \(AC\). Запишем теорему Пифагора для \(\triangle ABC\): \(BC^2 = AB^2 + AC^2\).
Из этой формулы выразим квадрат длины катета \(AC\): \(AC^2 = BC^2 — AB^2\). Подставим известные значения: \(AC^2 = 37^2 — 35^2\). Вычислим квадраты чисел: \(37^2 = 1369\) и \(35^2 = 1225\). Тогда \(AC^2 = 1369 — 1225 = 144\). Чтобы найти длину \(AC\), извлечем квадратный корень из \(144\): \(AC = \sqrt{144} = 12\) см.
Теперь, зная длины обоих катетов основания, вычислим площадь основания \(S_{\text{основания}}\): \(S_{\text{основания}} = \frac{1}{2} \cdot AB \cdot AC = \frac{1}{2} \cdot 35 \text{ см} \cdot 12 \text{ см}\). Выполним умножение: \(\frac{1}{2} \cdot 12 = 6\), затем \(35 \cdot 6 = 210\). Таким образом, площадь основания \(S_{\text{основания}} = 210\) см².
Высота прямой призмы равна длине бокового ребра. В данном случае высота \(h = AA_1 = 1,1\) дм. Для единообразия единиц измерения переведем дециметры в сантиметры, зная, что \(1\) дм \(= 10\) см. Следовательно, \(h = 1,1 \text{ дм} = 1,1 \cdot 10 \text{ см} = 11\) см.
Теперь, когда у нас есть площадь основания \(S_{\text{основания}} = 210\) см² и высота призмы \(h = 11\) см, мы можем вычислить объем призмы: \(V_{\text{призмы}} = S_{\text{основания}} \cdot h = 210 \text{ см}^2 \cdot 11 \text{ см}\). Выполним умножение: \(210 \cdot 11 = 2310\).
Таким образом, объем призмы \(V_{\text{призмы}} = 2310\) см³.
Ответ: Объем призмы равен \(2310\) см³.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!