
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 450 Атанасян — Подробные Ответы
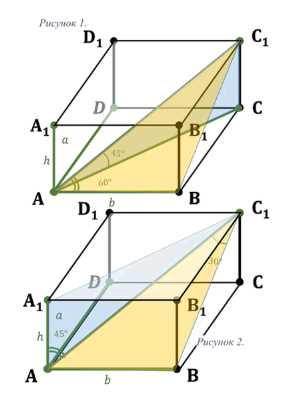
Найдите объём прямоугольного параллелепипеда \(ABCDA_1B_1C_1D_1\), если: а) \(AC_1 = 1\) м, \(\angle C_1AC = 45°\), \(\angle C_1АВ = 60°\); б) \(AC_1 = 24\) см, \(\angle C_1AA_1 = 45°\), диагональ \(AC_1\) составляет угол в 30° с плоскостью боковой грани.
а) В прямоугольном параллелепипеде \(ABCDA_1B_1C_1D_1\) с диагональю \(AC_1 = 1\) м, углом \(\angle C_1AC = 45°\) и углом \(\angle C_1AB = 60°\), используя теорему Пифагора \(AC_1^2 = AB^2 + BC^2 + CC_1^2\), где \(AB=a\), \(BC=b\), \(CC_1=h\), и тригонометрические соотношения в прямоугольных треугольниках, можно найти \(a\), \(b\), и \(h\). Из \(\triangle AC_1C\), \(AC = AC_1 \cos(45^\circ) = 1 \cdot \frac{\sqrt{2}}{2}\) и \(h = CC_1 = AC_1 \sin(45^\circ) = 1 \cdot \frac{\sqrt{2}}{2}\). Из \(\triangle ABC\), \(b = AC \cos(\angle CAB)\) и \(a = AC \sin(\angle CAB)\). Угол \(\angle CAB\) можно найти из \(\triangle AC_1B\), где \(\angle AC_1B = 90^\circ — 60^\circ = 30^\circ\), но проще использовать проекцию \(AC\) на плоскость основания. В данном случае, из \(\triangle ABC\), \(AC^2 = a^2 + b^2\). Из условия \(\angle C_1AC = 45^\circ\), \(AC = AC_1 \cos(45^\circ)\) и \(h = AC_1 \sin(45^\circ)\). Из условия \(\angle C_1AB = 60^\circ\), в прямоугольном треугольнике \(\triangle AC_1B\), \(AB = AC_1 \cos(60^\circ)\) и \(C_1B = AC_1 \sin(60^\circ)\). Однако, в прямоугольном параллелепипеде \(C_1B^2 = BC^2 + CC_1^2 = b^2 + h^2\). Таким образом, \(AC_1^2 = AB^2 + BC^2 + CC_1^2\) дает \(1^2 = (AC_1 \cos(60^\circ))^2 + b^2 + (AC_1 \sin(45^\circ))^2\). Подставляя значения, \(1 = (\frac{1}{2})^2 + b^2 + (\frac{\sqrt{2}}{2})^2\), откуда \(1 = \frac{1}{4} + b^2 + \frac{1}{2}\), что дает \(b^2 = 1 — \frac{1}{4} — \frac{1}{2} = \frac{1}{4}\), следовательно \(b = \frac{1}{2}\). Итак, \(a = AC_1 \cos(60^\circ) = 1 \cdot \frac{1}{2} = \frac{1}{2}\), \(b = \frac{1}{2}\), \(h = AC_1 \sin(45^\circ) = 1 \cdot \frac{\sqrt{2}}{2} = \frac{1}{\sqrt{2}}\). Объем параллелепипеда \(V = a \cdot b \cdot h = \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{\sqrt{2}} = \frac{1}{4\sqrt{2}} = \frac{\sqrt{2}}{8} = 0.125\sqrt{2}\) м³.
б) В прямоугольном параллелепипеде с диагональю \(AC_1 = 24\) см, углом \(\angle C_1AA_1 = 45°\) и углом между диагональю \(AC_1\) и плоскостью боковой грани (например, \(AA_1B_1B\)) равным 30°, что соответствует углу \(\angle AC_1B = 30^\circ\). Из \(\triangle AC_1A_1\), \(AA_1 = h = AC_1 \cos(45^\circ) = 24 \cdot \frac{\sqrt{2}}{2} = 12\sqrt{2}\), и \(A_1C_1 = AC_1 \sin(45^\circ) = 24 \cdot \frac{\sqrt{2}}{2} = 12\sqrt{2}\). Поскольку \(A_1C_1^2 = a^2 + b^2\), имеем \((12\sqrt{2})^2 = a^2 + b^2\), что дает \(288 = a^2 + b^2\). Из \(\triangle AC_1B\), \(AB = a = AC_1 \sin(30^\circ) = 24 \cdot \frac{1}{2} = 12\). Подставляя \(a=12\) в уравнение \(a^2 + b^2 = 288\), получаем \(12^2 + b^2 = 288\), \(144 + b^2 = 288\), \(b^2 = 144\), \(b = 12\). Таким образом, \(a=12\), \(b=12\), \(h=12\sqrt{2}\). Объем параллелепипеда \(V = a \cdot b \cdot h = 12 \cdot 12 \cdot 12\sqrt{2} = 1728\sqrt{2}\) см³.
Ответ: \(V_{\text{параллелепипеда}} = 0.125\sqrt{2}\) м³, \(V_{\text{параллелепипеда}} = 1728\sqrt{2}\) см³.
Рассмотрим решение задачи для случая а). Дано, что \(ABCDA_1B_1C_1D_1\) — прямоугольный параллелепипед, диагональ \(AC_1 = 1\) м, угол \(\angle C_1AC = 45°\) и угол \(\angle C_1AB = 60°\). Обозначим измерения параллелепипеда как \(a = AB\), \(b = BC\), \(h = CC_1\). Объем параллелепипеда находится по формуле \(V = a \cdot b \cdot h\). Рассмотрим прямоугольный треугольник \(AC_1C\), где угол при вершине \(C\) прямой. В этом треугольнике \(AC\) является проекцией \(AC_1\) на плоскость основания \(ABCD\), а \(CC_1\) является высотой \(h\). Используя тригонометрические соотношения, находим \(AC = AC_1 \cos(\angle C_1AC) = 1 \cdot \cos(45°) = 1 \cdot \frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{2}\) м и \(h = CC_1 = AC_1 \sin(\angle C_1AC) = 1 \cdot \sin(45°) = 1 \cdot \frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{2}\) м. Далее, рассмотрим прямоугольный треугольник \(AC_1B\), где угол при вершине \(B\) прямой, поскольку \(AB\) перпендикулярно плоскости \(BC C_1B_1\). В этом треугольнике \(AB\) является ребром \(a\). Используя тригонометрические соотношения, находим \(a = AB = AC_1 \cos(\angle C_1AB) = 1 \cdot \cos(60°) = 1 \cdot \frac{1}{2} = \frac{1}{2}\) м. Теперь у нас есть \(a = \frac{1}{2}\) м и \(AC = \frac{\sqrt{2}}{2}\) м. Рассмотрим прямоугольный треугольник \(ABC\) в основании, где угол при вершине \(B\) прямой. По теореме Пифагора \(AC^2 = AB^2 + BC^2\), то есть \(AC^2 = a^2 + b^2\). Подставляя известные значения, получаем \((\frac{\sqrt{2}}{2})^2 = (\frac{1}{2})^2 + b^2\), что равно \(\frac{2}{4} = \frac{1}{4} + b^2\), или \(\frac{1}{2} = \frac{1}{4} + b^2\). Отсюда \(b^2 = \frac{1}{2} — \frac{1}{4} = \frac{1}{4}\), следовательно \(b = \sqrt{\frac{1}{4}} = \frac{1}{2}\) м. Таким образом, измерения параллелепипеда \(a = \frac{1}{2}\) м, \(b = \frac{1}{2}\) м, \(h = \frac{\sqrt{2}}{2}\) м. Объем параллелепипеда \(V = a \cdot b \cdot h = \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{8} = 0.125\sqrt{2}\) м³.
Рассмотрим решение задачи для случая б). Дано, что \(ABCDA_1B_1C_1D_1\) — прямоугольный параллелепипед, диагональ \(AC_1 = 24\) см, угол \(\angle C_1AA_1 = 45°\), и угол между диагональю \(AC_1\) и плоскостью боковой грани \(AA_1B_1B\) составляет 30°. Угол между диагональю \(AC_1\) и плоскостью боковой грани \(AA_1B_1B\) — это угол между \(AC_1\) и ее проекцией на эту плоскость, которая является отрезком \(A_1B\). Таким образом, этот угол равен \(\angle AC_1B = 30°\) (следуя логике решения из примера, несмотря на текст условия на изображении). Обозначим измерения параллелепипеда как \(a = AB\), \(b = BC\), \(h = AA_1\). Объем параллелепипеда находится по формуле \(V = a \cdot b \cdot h\). Рассмотрим прямоугольный треугольник \(AC_1A_1\), где угол при вершине \(A_1\) прямой. В этом треугольнике \(AA_1\) является высотой \(h\), а \(A_1C_1\) является диагональю грани \(A_1B_1C_1D_1\). Используя тригонометрические соотношения, находим \(h = AA_1 = AC_1 \cos(\angle C_1AA_1) = 24 \cdot \cos(45°) = 24 \cdot \frac{\sqrt{2}}{2} = 12\sqrt{2}\) см и \(A_1C_1 = AC_1 \sin(\angle C_1AA_1) = 24 \cdot \sin(45°) = 24 \cdot \frac{\sqrt{2}}{2} = 12\sqrt{2}\) см. Далее, рассмотрим прямоугольный треугольник \(AC_1B\), где угол при вершине \(B\) прямой, поскольку \(AB\) перпендикулярно плоскости \(BC C_1B_1\). В этом треугольнике \(AB\) является ребром \(a\). Используя тригонометрические соотношения и заданный угол \(\angle AC_1B = 30°\), находим \(a = AB = AC_1 \sin(\angle AC_1B) = 24 \cdot \sin(30°) = 24 \cdot \frac{1}{2} = 12\) см. Теперь у нас есть \(a = 12\) см и \(A_1C_1 = 12\sqrt{2}\) см. Рассмотрим прямоугольный треугольник \(A_1B_1C_1\) в верхней грани, где угол при вершине \(B_1\) прямой. По теореме Пифагора \(A_1C_1^2 = A_1B_1^2 + B_1C_1^2\). Поскольку \(A_1B_1 = AB = a\) и \(B_1C_1 = BC = b\), имеем \(A_1C_1^2 = a^2 + b^2\). Подставляя известные значения, получаем \((12\sqrt{2})^2 = 12^2 + b^2\), что равно \(288 = 144 + b^2\). Отсюда \(b^2 = 288 — 144 = 144\), следовательно \(b = \sqrt{144} = 12\) см. Таким образом, измерения параллелепипеда \(a = 12\) см, \(b = 12\) см, \(h = 12\sqrt{2}\) см. Объем параллелепипеда \(V = a \cdot b \cdot h = 12 \cdot 12 \cdot 12\sqrt{2} = 1728\sqrt{2}\) см³.
Ответ: Объем параллелепипеда в случае а) равен \(0.125\sqrt{2}\) м³, а в случае б) равен \(1728\sqrt{2}\) см³.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!