ГДЗ по Геометрии 11 класс Номер 449 Атанасян — Подробные Ответы

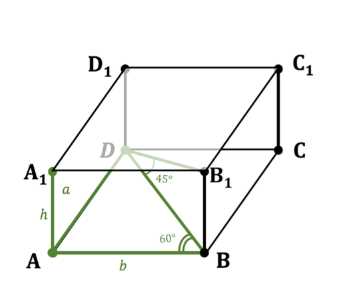
В прямоугольном параллелепипеде \(ABCDA_1B_1C_1D_1\) диагональ \(B_1D\) составляет с плоскостью основания угол в 45°, а двугранный угол \(A_1B_1BD\) равен 60°. Найдите объём параллелепипеда, если диагональ основания равна 12 см.

Объем прямоугольного параллелепипеда равен произведению его измерений: \(V = a \cdot b \cdot h\).
В прямоугольном треугольнике \(ABD\) с прямым углом при вершине \(A\), диагональ основания \(BD = 12\) см и угол \(\angle ABD = 60^\circ\). Используя тригонометрические соотношения, находим стороны основания: \(a = AB = BD \cdot \cos(60^\circ) = 12 \cdot \frac{1}{2} = 6\) см и \(b = AD = BD \cdot \sin(60^\circ) = 12 \cdot \frac{\sqrt{3}}{2} = 6\sqrt{3}\) см.
В прямоугольном треугольнике \(BDB_1\) с прямым углом при вершине \(B\), диагональ основания \(BD = 12\) см и угол \(\angle BDB_1 = 45^\circ\). Высота параллелепипеда \(h = BB_1 = BD \cdot \tan(45^\circ) = 12 \cdot 1 = 12\) см.
Объем параллелепипеда равен \(V = a \cdot b \cdot h = 6 \cdot 6\sqrt{3} \cdot 12 = 432\sqrt{3}\) см³.
Ответ: Объем параллелепипеда равен \(432\sqrt{3}\) см³.

Дано: прямоугольный параллелепипед \(ABCDA_1B_1C_1D_1\), диагональ основания \(BD = 12\) см, угол между диагональю параллелепипеда \(B_1D\) и плоскостью основания равен \(\angle BDB_1 = 45^\circ\), двугранный угол между плоскостью \(A_1B_1B\) и плоскостью \(DB_1B\) равен \(\angle A_1B_1BD = 60^\circ\).
Найти: Объем параллелепипеда \(V_{параллелепипеда}\).

Решение:
Объем прямоугольного параллелепипеда вычисляется по формуле \(V = a \cdot b \cdot h\), где \(a\) и \(b\) — длины сторон основания, а \(h\) — высота параллелепипеда.

Поскольку \(ABCDA_1B_1C_1D_1\) — прямоугольный параллелепипед, основание \(ABCD\) является прямоугольником. Угол между плоскостью \(A_1B_1B\) и плоскостью \(DB_1B\) — это двугранный угол при ребре \(B_1B\). Линейным углом этого двугранного угла является угол \(\angle ABD\), лежащий в плоскости основания и перпендикулярный ребру \(B_1B\) (или \(BB_1\)). Следовательно, \(\angle ABD = 60^\circ\).

Рассмотрим прямоугольный треугольник \(ABD\) в основании. Угол при вершине \(A\) прямой (\(\angle BAD = 90^\circ\)). Известна гипотенуза \(BD = 12\) см и угол \(\angle ABD = 60^\circ\).
Используя тригонометрические соотношения в прямоугольном треугольнике, найдем длины сторон основания \(a = AB\) и \(b = AD\).
Сторона \(a = AB\) прилежит к углу \(60^\circ\), поэтому \(a = BD \cdot \cos(\angle ABD) = 12 \cdot \cos(60^\circ)\).
Значение \(\cos(60^\circ) = \frac{1}{2}\), следовательно, \(a = 12 \cdot \frac{1}{2} = 6\) см.
Сторона \(b = AD\) противолежит углу \(60^\circ\), поэтому \(b = BD \cdot \sin(\angle ABD) = 12 \cdot \sin(60^\circ)\).
Значение \(\sin(60^\circ) = \frac{\sqrt{3}}{2}\), следовательно, \(b = 12 \cdot \frac{\sqrt{3}}{2} = 6\sqrt{3}\) см.

Теперь найдем высоту параллелепипеда \(h = BB_1\). Рассмотрим прямоугольный треугольник \(BDB_1\). Угол при вершине \(B\) прямой (\(\angle B_1BD = 90^\circ\)) так как \(BB_1\) перпендикулярно плоскости основания \(ABCD\), а \(BD\) лежит в этой плоскости. Известна сторона \(BD = 12\) см и угол \(\angle BDB_1 = 45^\circ\).
Высота \(h = BB_1\) противолежит углу \(45^\circ\), а сторона \(BD\) прилежит к этому углу. Используем тангенс угла: \(h = BD \cdot \tan(\angle BDB_1) = 12 \cdot \tan(45^\circ)\).
Значение \(\tan(45^\circ) = 1\), следовательно, \(h = 12 \cdot 1 = 12\) см.

Теперь, зная измерения параллелепипеда: \(a = 6\) см, \(b = 6\sqrt{3}\) см, \(h = 12\) см, вычислим его объем.
\(V_{параллелепипеда} = a \cdot b \cdot h = 6 \cdot (6\sqrt{3}) \cdot 12\).
Произведем умножение: \(V_{параллелепипеда} = 6 \cdot 6 \cdot 12 \cdot \sqrt{3} = 36 \cdot 12 \cdot \sqrt{3} = 432\sqrt{3}\) см³.

Ответ: Объем параллелепипеда равен \(432\sqrt{3}\) см³.