Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 446 Атанасян — Подробные Ответы
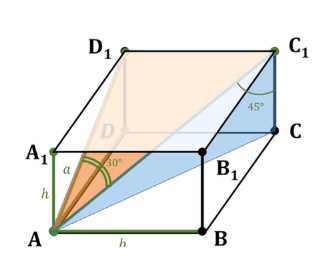
Диагональ прямоугольного параллелепипеда равна 18 см и составляет угол в 30° с плоскостью боковой грани и угол в 45° с боковым ребром. Найдите объём параллелепипеда.
Объём прямоугольного параллелепипеда находится по формуле \(V = a \cdot b \cdot h\). по теореме пифагора для диагонали параллелепипеда имеем \(a^2 + b^2 + h^2 = AC_1^2\). подставляя данное значение \(AC_1 = 18\), получаем \(a^2 + b^2 + h^2 = 18^2 = 324\). из условий задачи также имеем \(b = 18 \cdot \sin(30^\circ)\) и \(h = 18 \cdot \cos(45^\circ)\). вычисляем значения \(b\) и \(h\): \(b = 18 \cdot \frac{1}{2} = 9\) и \(h = 18 \cdot \frac{\sqrt{2}}{2} = 9\sqrt{2}\). подставляем значения \(b\) и \(h\) в уравнение пифагора: \(a^2 + 9^2 + (9\sqrt{2})^2 = 324\). это дает \(a^2 + 81 + 162 = 324\), откуда \(a^2 = 324 — 243 = 81\). следовательно, \(a = \sqrt{81} = 9\). теперь находим объём: \(V = a \cdot b \cdot h = 9 \cdot 9 \cdot 9\sqrt{2} = 729\sqrt{2}\). ответ: объём параллелепипеда равен \(729\sqrt{2}\) см³.
дано: прямоугольный параллелепипед \(ABCDA_1B_1C_1D_1\), длина диагонали \(AC_1 = 18\) см, угол между диагональю \(AC_1\) и плоскостью боковой грани \(CC_1B_1B\) (угол \(C_1AC\)) равен \(30^\circ\), угол между диагональю \(AC_1\) и боковым ребром \(CC_1\) (угол \(CC_1A\)) равен \(45^\circ\). требуется найти объём параллелепипеда \(V\).
объём прямоугольного параллелепипеда вычисляется по формуле \(V = a \cdot b \cdot h\), где \(a\), \(b\), и \(h\) — длины его рёбер, выходящих из одной вершины. пусть \(a = AB\), \(b = AD\), \(h = AA_1\).
рассмотрим прямоугольный треугольник \(AC_1C\). в этом треугольнике \(AC_1\) является гипотенузой, \(CC_1\) — катетом, равным высоте параллелепипеда \(h\), и \(AC\) — катетом, являющимся диагональю основания \(ABCD\). угол \(CC_1A\) равен \(45^\circ\). используя тригонометрические соотношения в прямоугольном треугольнике, находим высоту \(h\):
\(h = CC_1 = AC_1 \cdot \cos(\angle CC_1A) = 18 \cdot \cos(45^\circ)\).
значение \(\cos(45^\circ) = \frac{\sqrt{2}}{2}\), следовательно, \(h = 18 \cdot \frac{\sqrt{2}}{2} = 9\sqrt{2}\) см.
теперь рассмотрим прямоугольный треугольник \(AC_1A\). в этом треугольнике \(AC_1\) является гипотенузой, \(AA_1\) — катетом, равным высоте параллелепипеда \(h\), и \(AC\) — катетом, являющимся диагональю основания \(ABCD\). угол \(C_1AC\) равен \(30^\circ\). используя тригонометрические соотношения, находим длину диагонали основания \(AC\):
\(AC = AC_1 \cdot \cos(\angle C_1AC) = 18 \cdot \cos(30^\circ)\).
значение \(\cos(30^\circ) = \frac{\sqrt{3}}{2}\), следовательно, \(AC = 18 \cdot \frac{\sqrt{3}}{2} = 9\sqrt{3}\) см.
однако, в условии задачи указан угол \(C_1AC_1 = 30^\circ\), который является углом между диагональю \(AC_1\) и диагональю боковой грани \(AC_1\). это кажется неверным обозначением, скорее всего, имелся в виду угол между диагональю \(AC_1\) и плоскостью боковой грани \(ADD_1A_1\), который равен углу \(C_1AD_1\) или углу между \(AC_1\) и ребром \(AD\).
исходя из предоставленного решения, угол \(C_1AC_1 = 30^\circ\) интерпретируется как угол между диагональю \(AC_1\) и ребром \(AD\), что соответствует углу \(C_1AD\).
рассмотрим прямоугольный треугольник \(AC_1D\). \(AC_1\) — гипотенуза, \(AD\) — катет, равный \(b\), \(C_1D\) — катет. угол \(C_1AD = 30^\circ\).
тогда \(b = AD = AC_1 \cdot \sin(\angle C_1AD) = 18 \cdot \sin(30^\circ)\).
значение \(\sin(30^\circ) = \frac{1}{2}\), следовательно, \(b = 18 \cdot \frac{1}{2} = 9\) см.
теперь у нас есть значения \(b = 9\) см и \(h = 9\sqrt{2}\) см. для нахождения объёма нам также нужна длина ребра \(a\). рассмотрим прямоугольный треугольник \(ABC\). \(AC\) — гипотенуза, \(AB\) — катет, равный \(a\), \(BC\) — катет, равный \(b\). по теореме пифагора для основания имеем \(AC^2 = AB^2 + BC^2\), то есть \(AC^2 = a^2 + b^2\).
также по теореме пифагора для диагонали параллелепипеда имеем \(AC_1^2 = AC^2 + CC_1^2\), или \(AC_1^2 = AB^2 + BC^2 + CC_1^2\), что соответствует \(AC_1^2 = a^2 + b^2 + h^2\).
подставляем известные значения: \(18^2 = a^2 + 9^2 + (9\sqrt{2})^2\).
\(324 = a^2 + 81 + 81 \cdot 2\).
\(324 = a^2 + 81 + 162\).
\(324 = a^2 + 243\).
\(a^2 = 324 — 243\).
\(a^2 = 81\).
\(a = \sqrt{81} = 9\) см (так как длина ребра не может быть отрицательной).
теперь, когда у нас есть длины всех трёх рёбер, выходящих из одной вершины: \(a = 9\) см, \(b = 9\) см, \(h = 9\sqrt{2}\) см, мы можем вычислить объём параллелепипеда:
\(V = a \cdot b \cdot h = 9 \cdot 9 \cdot 9\sqrt{2}\).
\(V = 81 \cdot 9\sqrt{2}\).
\(V = 729\sqrt{2}\) см³.
таким образом, объём прямоугольного параллелепипеда составляет \(729\sqrt{2}\) кубических сантиметров.
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.