Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 445 Атанасян — Подробные Ответы
Найдите объём прямоугольного параллелепипеда \(ABCDA_1B_1C_1D_1\), если \(AC_1 = 13\) см, \(BD = 12\) см и \(BC_1 = 11\) см.
Дано: прямоугольный параллелепипед \(ABCDA_1B_1C_1D_1\), \(AC_1 = 13\) см, \(BD = 12\) см, \(BC_1 = 11\) см. Найти: \(V_{\text{параллелепипеда}}\). Решение: \(V_{\text{параллелепипеда}} = a \cdot b \cdot h\). По теореме Пифагора из условия задачи имеем систему уравнений: \(\begin{cases} a^2 + b^2 + h^2 = 169 \\ a^2 + b^2 = 144 \\ a^2 + h^2 = 121 \end{cases}\) \(\Rightarrow \begin{cases} h^2 = 169 — 144 \\ a^2 + b^2 = 144 \\ a^2 + h^2 = 121 \end{cases} \Rightarrow \begin{cases} h = 5 \\ a^2 + b^2 = 144 \\ a^2 + h^2 = 121 \end{cases}\) \(\Rightarrow \begin{cases} h = 5 \\ a^2 + b^2 = 144 \\ a^2 + 5^2 = 121 \end{cases} \Rightarrow \begin{cases} h = 5 \\ a^2 + b^2 = 144 \\ a^2 = 96 \end{cases}\) \(\Rightarrow \begin{cases} h = 5 \\ b^2 = 144 — 96 \\ a^2 = 96 \end{cases} \Rightarrow \begin{cases} h = 5 \\ b^2 = 48 \\ a^2 = 96 \end{cases} \Rightarrow \begin{cases} h = 5 \\ b = \sqrt{48} \\ a = \sqrt{96} \end{cases}\) \(V_{\text{параллелепипеда}} = 5 \cdot \sqrt{48} \cdot \sqrt{96} = 5 \cdot \sqrt{48 \cdot 96} = 5 \cdot \sqrt{4608} = 5 \cdot 48\sqrt{2} = 240\sqrt{2}\) см³. Ответ: \(V_{\text{параллелепипеда}} = 240\sqrt{2}\) см³.
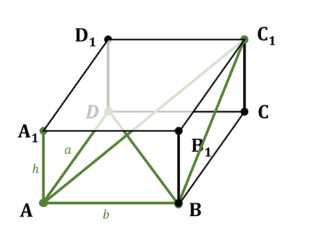
Дано: прямоугольный параллелепипед \(ABCDA_1B_1C_1D_1\). Известны длины трех диагоналей: диагональ параллелепипеда \(AC_1 = 13\) см, диагональ основания \(BD = 12\) см, и диагональ боковой грани \(BC_1 = 11\) см. Необходимо найти объем параллелепипеда \(V_{\text{параллелепипеда}}\).
Объем прямоугольного параллелепипеда находится по формуле \(V = a \cdot b \cdot h\), где \(a\), \(b\), и \(h\) — длины ребер параллелепипеда, выходящих из одной вершины. Пусть \(AB = a\), \(AD = b\), и \(AA_1 = h\).
Рассмотрим диагонали и ребра параллелепипеда, используя теорему Пифагора.
Диагональ основания \(BD\) связана с ребрами основания \(AB\) и \(AD\). В прямоугольнике \(ABCD\) по теореме Пифагора \(BD^2 = AB^2 + AD^2\). Подставляя известные значения, получаем \(12^2 = a^2 + b^2\), что дает уравнение \(a^2 + b^2 = 144\).
Диагональ боковой грани \(BC_1\) связана с ребром основания \(BC\) и ребром \(CC_1\). В прямоугольнике \(BCC_1B_1\) по теореме Пифагора \(BC_1^2 = BC^2 + CC_1^2\). Поскольку \(BC = AD = b\) и \(CC_1 = AA_1 = h\), получаем \(11^2 = b^2 + h^2\), что дает уравнение \(b^2 + h^2 = 121\).
Диагональ параллелепипеда \(AC_1\) связана с ребрами \(AB\), \(AD\), и \(AA_1\). В прямоугольном параллелепипеде квадрат длины диагонали равен сумме квадратов длин всех трех измерений: \(AC_1^2 = AB^2 + AD^2 + AA_1^2\). Подставляя известные значения, получаем \(13^2 = a^2 + b^2 + h^2\), что дает уравнение \(a^2 + b^2 + h^2 = 169\).
Таким образом, мы получили систему из трех уравнений с тремя неизвестными \(a^2\), \(b^2\), и \(h^2\):
\( \begin{cases} a^2 + b^2 + h^2 = 169 \\ a^2 + b^2 = 144 \\ b^2 + h^2 = 121 \end{cases} \)
Решим эту систему. Подставим второе уравнение \(a^2 + b^2 = 144\) в первое уравнение:
\(144 + h^2 = 169\)
Вычтем 144 из обеих частей уравнения, чтобы найти \(h^2\):
\(h^2 = 169 — 144\)
\(h^2 = 25\)
Извлечем квадратный корень, чтобы найти \(h\). Поскольку длина ребра положительна, берем положительный корень:
\(h = \sqrt{25}\)
\(h = 5\) см.
Теперь у нас есть значение \(h^2 = 25\). Подставим это значение в третье уравнение системы \(b^2 + h^2 = 121\):
\(b^2 + 25 = 121\)
Вычтем 25 из обеих частей уравнения, чтобы найти \(b^2\):
\(b^2 = 121 — 25\)
\(b^2 = 96\)
Извлечем квадратный корень, чтобы найти \(b\):
\(b = \sqrt{96}\) см.
Теперь у нас есть значения \(h^2 = 25\) и \(b^2 = 96\). Подставим значение \(b^2 = 96\) во второе уравнение системы \(a^2 + b^2 = 144\):
\(a^2 + 96 = 144\)
Вычтем 96 из обеих частей уравнения, чтобы найти \(a^2\):
\(a^2 = 144 — 96\)
\(a^2 = 48\)
Извлечем квадратный корень, чтобы найти \(a\):
\(a = \sqrt{48}\) см.
Теперь у нас есть длины всех трех ребер: \(a = \sqrt{48}\) см, \(b = \sqrt{96}\) см, и \(h = 5\) см.
Вычислим объем параллелепипеда \(V = a \cdot b \cdot h\):
\(V = \sqrt{48} \cdot \sqrt{96} \cdot 5\)
Умножим корни: \(\sqrt{48} \cdot \sqrt{96} = \sqrt{48 \cdot 96}\).
Вычислим произведение под корнем: \(48 \cdot 96 = 4608\).
\(V = 5 \cdot \sqrt{4608}\)
Упростим квадратный корень из 4608. Разложим 4608 на множители: \(4608 = 2 \cdot 2304 = 2 \cdot 48^2\).
\(V = 5 \cdot \sqrt{2 \cdot 48^2}\)
Вынесем \(48^2\) из-под корня:
\(V = 5 \cdot 48 \cdot \sqrt{2}\)
Вычислим произведение: \(5 \cdot 48 = 240\).
\(V = 240\sqrt{2}\) см³.
Ответ: Объем прямоугольного параллелепипеда равен \(240\sqrt{2}\) см³.
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.