ГДЗ по Геометрии 11 класс Номер 443 Атанасян — Подробные Ответы

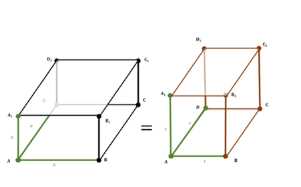
Измерения прямоугольного параллелепипеда равны 8 см, 12 см и 18 см. Найдите ребро куба, объём которого равен объёму этого параллелепипеда.

Обозначим сторону куба за \(x\). Объем куба равен \(V_{куба} = x^3\).

Измерения прямоугольного параллелепипеда равны \(a = 8\) см, \(b = 12\) см, \(h = 18\) см. Объем прямоугольного параллелепипеда равен \(V_{параллелепипеда} = a \cdot b \cdot h\). По условию, объем куба равен объему параллелепипеда: \(V_{куба} = V_{параллелепипеда}\). Следовательно, \(x^3 = a \cdot b \cdot h\). Подставляем значения измерений параллелепипеда: \(x^3 = 8 \cdot 12 \cdot 18\). Вычисляем произведение: \(x^3 = 1728\). Чтобы найти сторону куба \(x\), необходимо извлечь кубический корень из 1728: \(x = \sqrt[3]{1728}\). Разложим числа на простые множители: \(8 = 2^3\), \(12 = 2^2 \cdot 3\), \(18 = 2 \cdot 3^2\). Тогда \(x^3 = 2^3 \cdot (2^2 \cdot 3) \cdot (2 \cdot 3^2) = 2^{3+2+1} \cdot 3^{1+2} = 2^6 \cdot 3^3\). Извлекая кубический корень, получаем \(x = \sqrt[3]{2^6 \cdot 3^3} = (2^6)^{1/3} \cdot (3^3)^{1/3} = 2^{6/3} \cdot 3^{3/3} = 2^2 \cdot 3^1 = 4 \cdot 3 = 12\). Таким образом, сторона куба равна 12 см. Ответ: 12 см.

Дано, что имеется куб со стороной, обозначенной как \(x\), и прямоугольный параллелепипед с измерениями 8 см, 12 см и 18 см. Также дано условие, что объем куба равен объему прямоугольного параллелепипеда. Необходимо найти значение стороны куба \(x\).

Объем куба вычисляется по формуле \(V_{куба} = x^3\), где \(x\) — длина стороны куба.

Объем прямоугольного параллелепипеда вычисляется по формуле \(V_{параллелепипеда} = a \cdot b \cdot h\), где \(a, b, h\) — длины его измерений. В данном случае измерения параллелепипеда равны 8 см, 12 см и 18 см.

Согласно условию задачи, объем куба равен объему прямоугольного параллелепипеда, что можно записать как \(V_{куба} = V_{параллелепипеда}\).

Подставляя формулы объемов, получаем уравнение: \(x^3 = a \cdot b \cdot h\).

Теперь подставим численные значения измерений параллелепипеда в это уравнение: \(x^3 = 8 \cdot 12 \cdot 18\).

Вычислим произведение в правой части уравнения:
\(8 \cdot 12 = 96\)
\(96 \cdot 18\). Умножим 96 на 18. \(96 \cdot 18 = (100 — 4) \cdot 18 = 100 \cdot 18 — 4 \cdot 18 = 1800 — 72 = 1728\).
Таким образом, получаем уравнение \(x^3 = 1728\).

Для того чтобы найти сторону куба \(x\), необходимо извлечь кубический корень из числа 1728: \(x = \sqrt[3]{1728}\).

Найдем кубический корень из 1728. Для этого можно разложить число 1728 на простые множители.
\(1728 \div 2 = 864\)
\(864 \div 2 = 432\)
\(432 \div 2 = 216\)
\(216 \div 2 = 108\)
\(108 \div 2 = 54\)
\(54 \div 2 = 27\)
\(27 \div 3 = 9\)
\(9 \div 3 = 3\)
\(3 \div 3 = 1\)
Таким образом, разложение числа 1728 на простые множители имеет вид \(1728 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 3 = 2^6 \cdot 3^3\).

Теперь подставим это разложение под знак кубического корня: \(x = \sqrt[3]{2^6 \cdot 3^3}\).

Используя свойство корней \(\sqrt[n]{a^m} = a^{m/n}\) и свойство корней \(\sqrt[n]{ab} = \sqrt[n]{a} \cdot \sqrt[n]{b}\), можем записать:
\(x = \sqrt[3]{2^6} \cdot \sqrt[3]{3^3}\)
\(x = 2^{6/3} \cdot 3^{3/3}\)
\(x = 2^2 \cdot 3^1\)
\(x = 4 \cdot 3\)
\(x = 12\).

Следовательно, длина стороны куба равна 12 см.

Ответ: 12 см.