Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 442 Атанасян — Подробные Ответы
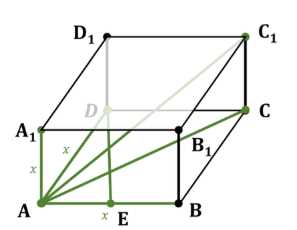
Найдите объём куба \(ABCDA_1B_1C_1D_1\), если: а) \(AC = 12\) см; б) \(AC_1 = 3\sqrt{2}\) м; в) \(DE = 1\) см, где Е — середина ребра АВ.
Обозначим сторону куба за \(x\). Объем куба равен \(V = x^3\).
а) Диагональ грани куба равна \(x\sqrt{2}\). По условию \(AC = 12\) см, значит \(x\sqrt{2} = 12\), откуда \(x = \frac{12}{\sqrt{2}} = 6\sqrt{2}\) см. Объем \(V = (6\sqrt{2})^3 = 216 \cdot 2\sqrt{2} = 432\sqrt{2}\) см³.
б) Диагональ куба равна \(x\sqrt{3}\). По условию \(AC_1 = 3\sqrt{2}\) м, значит \(x\sqrt{3} = 3\sqrt{2}\), откуда \(x = \frac{3\sqrt{2}}{\sqrt{3}} = \sqrt{6}\) м. Объем \(V = (\sqrt{6})^3 = 6\sqrt{6}\) м³.
в) E — середина ребра AB, DE = 1 см. В прямоугольном треугольнике ADE катеты AD = \(x\), AE = \(x/2\). По теореме Пифагора \(DE^2 = AD^2 + AE^2\), то есть \(1^2 = x^2 + (x/2)^2 = x^2 + x^2/4 = \frac{5x^2}{4}\). Отсюда \(5x^2 = 4\), \(x^2 = \frac{4}{5}\), \(x = \sqrt{\frac{4}{5}} = \frac{2}{\sqrt{5}}\) см. Объем \(V = x^3 = \left(\frac{2}{\sqrt{5}}\right)^3 = \frac{8}{5\sqrt{5}} = \frac{8\sqrt{5}}{25} = 0.32\sqrt{5}\) см³.
Ответ: \(432\sqrt{2}\) см³, \(6\sqrt{6}\) м³, \(0.32\sqrt{5}\) см³.
Обозначим сторону куба за \(x\). Объем куба \(V\) находится по формуле \(V = x^3\). Для нахождения объема в каждом случае необходимо сначала определить значение стороны куба \(x\).
а) Дана длина диагонали грани куба \(AC = 12\) см. Диагональ грани куба является гипотенузой прямоугольного треугольника со сторонами, равными ребру куба. По теореме Пифагора, квадрат диагонали грани равен сумме квадратов двух сторон куба, лежащих в этой грани. То есть, \(AC^2 = AB^2 + BC^2\). Поскольку \(AB = BC = x\), получаем \(AC^2 = x^2 + x^2 = 2x^2\). Извлекая квадратный корень, находим длину диагонали грани: \(AC = \sqrt{2x^2} = x\sqrt{2}\). Зная, что \(AC = 12\), составляем уравнение \(x\sqrt{2} = 12\). Чтобы найти \(x\), делим обе части на \(\sqrt{2}\): \(x = \frac{12}{\sqrt{2}}\). Для избавления от иррациональности в знаменателе, умножим числитель и знаменатель на \(\sqrt{2}\): \(x = \frac{12 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{12\sqrt{2}}{2} = 6\sqrt{2}\) см. Теперь вычислим объем куба, подставив найденное значение \(x\) в формулу объема: \(V = x^3 = (6\sqrt{2})^3\). Возведем в куб: \(V = 6^3 \cdot (\sqrt{2})^3 = 216 \cdot (\sqrt{2})^2 \cdot \sqrt{2} = 216 \cdot 2 \cdot \sqrt{2} = 432\sqrt{2}\) см³.
б) Дана длина диагонали куба \(AC_1 = 3\sqrt{2}\) м. Диагональ куба \(AC_1\) является гипотенузой прямоугольного треугольника \(ACC_1\), где \(AC\) — диагональ грани, а \(CC_1\) — ребро куба. Длина диагонали грани \(AC = x\sqrt{2}\), а длина ребра \(CC_1 = x\). По теореме Пифагора для треугольника \(ACC_1\): \(AC_1^2 = AC^2 + CC_1^2\). Подставляя выражения через \(x\): \(AC_1^2 = (x\sqrt{2})^2 + x^2 = 2x^2 + x^2 = 3x^2\). Извлекая квадратный корень, находим длину диагонали куба: \(AC_1 = \sqrt{3x^2} = x\sqrt{3}\). Зная, что \(AC_1 = 3\sqrt{2}\), составляем уравнение \(x\sqrt{3} = 3\sqrt{2}\). Чтобы найти \(x\), делим обе части на \(\sqrt{3}\): \(x = \frac{3\sqrt{2}}{\sqrt{3}}\). Для избавления от иррациональности в знаменателе, умножим числитель и знаменатель на \(\sqrt{3}\): \(x = \frac{3\sqrt{2} \cdot \sqrt{3}}{\sqrt{3} \cdot \sqrt{3}} = \frac{3\sqrt{6}}{3} = \sqrt{6}\) м. Теперь вычислим объем куба: \(V = x^3 = (\sqrt{6})^3\). Возведем в куб: \(V = (\sqrt{6})^2 \cdot \sqrt{6} = 6\sqrt{6}\) м³.
в) Дана длина отрезка \(DE = 1\) см, где E — середина ребра AB. Поскольку E — середина ребра AB, длина отрезка \(AE\) равна половине длины ребра куба: \(AE = \frac{AB}{2} = \frac{x}{2}\). Рассмотрим прямоугольный треугольник \(ADE\). Катетами этого треугольника являются ребро \(AD\) и отрезок \(AE\). Длина ребра \(AD = x\), длина отрезка \(AE = \frac{x}{2}\). Гипотенузой является отрезок \(DE\). По теореме Пифагора для треугольника \(ADE\): \(DE^2 = AD^2 + AE^2\). Подставляем известные значения: \(1^2 = x^2 + \left(\frac{x}{2}\right)^2\). Упрощаем: \(1 = x^2 + \frac{x^2}{4}\). Приводим к общему знаменателю: \(1 = \frac{4x^2}{4} + \frac{x^2}{4} = \frac{5x^2}{4}\). Теперь решаем уравнение относительно \(x^2\): \(5x^2 = 4\), откуда \(x^2 = \frac{4}{5}\). Извлекаем квадратный корень, чтобы найти \(x\): \(x = \sqrt{\frac{4}{5}}\). Поскольку \(x\) — длина, берем положительное значение: \(x = \frac{\sqrt{4}}{\sqrt{5}} = \frac{2}{\sqrt{5}}\) см. Для избавления от иррациональности в знаменателе, умножим числитель и знаменатель на \(\sqrt{5}\): \(x = \frac{2 \cdot \sqrt{5}}{\sqrt{5} \cdot \sqrt{5}} = \frac{2\sqrt{5}}{5}\) см. Теперь вычислим объем куба: \(V = x^3 = \left(\frac{2}{\sqrt{5}}\right)^3\). Возведем в куб: \(V = \frac{2^3}{(\sqrt{5})^3} = \frac{8}{(\sqrt{5})^2 \cdot \sqrt{5}} = \frac{8}{5\sqrt{5}}\). Для избавления от иррациональности в знаменателе, умножим числитель и знаменатель на \(\sqrt{5}\): \(V = \frac{8 \cdot \sqrt{5}}{5\sqrt{5} \cdot \sqrt{5}} = \frac{8\sqrt{5}}{5 \cdot 5} = \frac{8\sqrt{5}}{25}\) см³. Переведем дробь в десятичную форму: \(\frac{8}{25} = 0.32\). Таким образом, \(V = 0.32\sqrt{5}\) см³.
Ответы для каждого случая соответственно: \(432\sqrt{2}\) см³, \(6\sqrt{6}\) м³, \(0.32\sqrt{5}\) см³.
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.