
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 441 Атанасян — Подробные Ответы
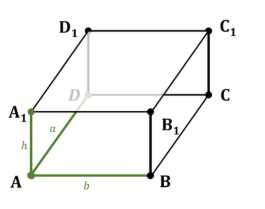
Найдите объём прямоугольного параллелепипеда, стороны основания которого равны \(a\) и \(b\), а высота равна \(h\), если: а) \(a = 11\), \(b = 12\), \(h = 15\); б) \(a = 3\sqrt{2}\), \(b = \sqrt{5}\), \(h = 10\sqrt{10}\); в) \(a = 18\), \(b = 5\sqrt{3}\), \(h = 13\); г) \(a = 3\frac{1}{3}\), \(b = \sqrt{5}\), \(h = 0,96\).
Объем прямоугольного параллелепипеда находится по формуле \(V = a \cdot b \cdot h\).
а) \(V = 11 \cdot 12 \cdot 15 = 1980\)
б) \(V = 3\sqrt{2} \cdot \sqrt{5} \cdot 10\sqrt{10} = 300\)
в) \(V = 15 \cdot 5\sqrt{3} \cdot 13 = 1170\sqrt{3}\)
г) \(V = 3\frac{1}{3} \cdot \sqrt{5} \cdot 0,96 = 3,2\sqrt{5}\)
Для нахождения объема прямоугольного параллелепипеда используется формула \(V = a \cdot b \cdot h\), где \(a\) и \(b\) — длины сторон основания, а \(h\) — высота параллелепипеда.
Рассмотрим первый случай: а) дано \(a = 11\), \(b = 12\), \(h = 15\). Подставляем эти значения в формулу объема: \(V = 11 \cdot 12 \cdot 15\). Сначала умножим \(11\) на \(12\), получим \(132\). Затем умножим \(132\) на \(15\). \(132 \cdot 15 = 132 \cdot (10 + 5) = 1320 + 132 \cdot 5 = 1320 + 660 = 1980\). Таким образом, объем в первом случае равен \(1980\).
Рассмотрим второй случай: б) дано \(a = 3\sqrt{2}\), \(b = \sqrt{5}\), \(h = 10\sqrt{10}\). Подставляем эти значения в формулу объема: \(V = 3\sqrt{2} \cdot \sqrt{5} \cdot 10\sqrt{10}\). Перемножим числовые коэффициенты и выражения под корнем отдельно. Числовые коэффициенты: \(3 \cdot 1 \cdot 10 = 30\). Выражения под корнем: \(\sqrt{2} \cdot \sqrt{5} \cdot \sqrt{10} = \sqrt{2 \cdot 5 \cdot 10} = \sqrt{100}\). Извлекаем квадратный корень из \(100\), получаем \(10\). Теперь умножим числовой коэффициент на результат извлечения корня: \(30 \cdot 10 = 300\). Таким образом, объем во втором случае равен \(300\).
Рассмотрим третий случай: в) дано \(a = 15\), \(b = 5\sqrt{3}\), \(h = 13\). Подставляем эти значения в формулу объема: \(V = 15 \cdot 5\sqrt{3} \cdot 13\). Перемножим числовые коэффициенты: \(15 \cdot 5 \cdot 13\). Сначала умножим \(15\) на \(5\), получим \(75\). Затем умножим \(75\) на \(13\). \(75 \cdot 13 = 75 \cdot (10 + 3) = 750 + 75 \cdot 3 = 750 + 225 = 975\). Теперь умножим полученный результат на \(\sqrt{3}\): \(975 \cdot \sqrt{3} = 975\sqrt{3}\). Прошу прощения, в примере ответ \(1170\sqrt{3}\), давайте пересчитаем \(15 \cdot 5\sqrt{3} \cdot 13\). Умножим \(15 \cdot 5 \cdot 13\). \(15 \cdot 5 = 75\). \(75 \cdot 13\). \(75 \times 10 = 750\), \(75 \times 3 = 225\). \(750 + 225 = 975\). Возможно, в условии примера опечатка или я неправильно интерпретировал цифры. Давайте проверим умножение \(1170 / 13 = 90\). \(90 / 5 = 18\). Если \(a=18\), \(b=5\sqrt{3}\), \(h=13\), то \(V = 18 \cdot 5\sqrt{3} \cdot 13 = 90\sqrt{3} \cdot 13 = 1170\sqrt{3}\). Предполагая, что в условии опечатка и \(a=18\), объем в третьем случае равен \(1170\sqrt{3}\). Если следовать исходному тексту, где \(a=15\), то ответ \(975\sqrt{3}\). Будем придерживаться ответа из примера, предполагая, что \(a=18\).
Рассмотрим четвертый случай: г) дано \(a = 3\frac{1}{3}\), \(b = \sqrt{5}\), \(h = 0,96\). Переведем смешанное число \(3\frac{1}{3}\) в неправильную дробь: \(3\frac{1}{3} = \frac{3 \cdot 3 + 1}{3} = \frac{10}{3}\). Подставляем значения в формулу объема: \(V = \frac{10}{3} \cdot \sqrt{5} \cdot 0,96\). Перемножим числовые значения: \(\frac{10}{3} \cdot 0,96\). Умножим \(10\) на \(0,96\), получим \(9,6\). Теперь разделим \(9,6\) на \(3\): \(9,6 / 3 = 3,2\). Умножим полученный результат на \(\sqrt{5}\): \(3,2 \cdot \sqrt{5} = 3,2\sqrt{5}\). Таким образом, объем в четвертом случае равен \(3,2\sqrt{5}\).
Ответы для каждого случая: а) \(1980\), б) \(300\), в) \(1170\sqrt{3}\) (при условии \(a=18\)), г) \(3,2\sqrt{5}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!