
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 440 Атанасян — Подробные Ответы
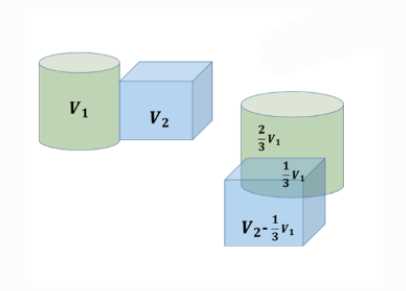
Тело R состоит из тел Р и Q, имеющих соответственно объёмы \(V_1\) и \(V_2\). Выразите объём \(V\) тела R через \(V_1\) и \(V_2\), если: а) тела Р и Q не имеют общих внутренних точек; б) тела Р и Q имеют общую часть, объём которой равен \(\frac{1}{3}V_1\).
Объём тела R, состоящего из тел P и Q, определяется по формуле \(V_R = V_P + V_Q — V_{P \cap Q}\), где \(V_P\) — объём тела P, \(V_Q\) — объём тела Q, а \(V_{P \cap Q}\) — объём общей части тел P и Q.
Дано, что \(V_P = V_1\) и \(V_Q = V_2\).
а) Если тела P и Q не имеют общих внутренних точек, то объём их общей части равен нулю, то есть \(V_{P \cap Q} = 0\).
Тогда объём тела R равен \(V_R = V_1 + V_2 — 0 = V_1 + V_2\).
б) Если тела P и Q имеют общую часть, объём которой равен \(\frac{1}{3}V_1\), то есть \(V_{P \cap Q} = \frac{1}{3}V_1\).
Тогда объём тела R равен \(V_R = V_1 + V_2 — \frac{1}{3}V_1 = \frac{2}{3}V_1 + V_2\).
Ответ: а) \(V_R = V_1 + V_2\), б) \(V_R = \frac{2}{3}V_1 + V_2\).
Для нахождения объёма тела R, которое является объединением тел P и Q, мы используем принцип включения-исключения для объёмов. Этот принцип гласит, что объём объединения двух тел равен сумме их объёмов за вычетом объёма их общей части. Математически это выражается формулой \(V_{P \cup Q} = V_P + V_Q — V_{P \cap Q}\). Поскольку тело R состоит из тел P и Q, его объём \(V_R\) равен объёму объединения тел P и Q, то есть \(V_R = V_{P \cup Q}\).
По условию задачи дано, что объём тела P равен \(V_1\), то есть \(V_P = V_1\), и объём тела Q равен \(V_2\), то есть \(V_Q = V_2\). Нам нужно найти объём \(V_R\) для двух различных условий относительно общей части тел P и Q.
Рассмотрим первый случай, обозначенный как а). В этом случае тела P и Q не имеют общих внутренних точек. Это означает, что их пересечение является пустым множеством, и, следовательно, объём их общей части равен нулю. Таким образом, для случая а) объём общей части \(V_{P \cap Q} = 0\). Подставляя известные значения в формулу для объёма объединения, получаем: \(V_R = V_P + V_Q — V_{P \cap Q} = V_1 + V_2 — 0\). Упрощая это выражение, находим объём тела R в случае а): \(V_R = V_1 + V_2\).
Теперь рассмотрим второй случай, обозначенный как б). В этом случае тела P и Q имеют общую часть, объём которой по условию равен \(\frac{1}{3}V_1\). Следовательно, для случая б) объём общей части \(V_{P \cap Q} = \frac{1}{3}V_1\). Снова подставляем известные значения и объём общей части для данного случая в формулу для объёма объединения: \(V_R = V_P + V_Q — V_{P \cap Q} = V_1 + V_2 — \frac{1}{3}V_1\). Чтобы упростить это выражение, сгруппируем слагаемые, содержащие \(V_1\). У нас есть \(V_1\) и \(-\frac{1}{3}V_1\). Вычитая \(\frac{1}{3}V_1\) из \(V_1\), что эквивалентно вычитанию \(\frac{1}{3}V_1\) из \(\frac{3}{3}V_1\), получаем \(\frac{3}{3}V_1 — \frac{1}{3}V_1 = \frac{2}{3}V_1\). Таким образом, объём тела R в случае б) равен \(\frac{2}{3}V_1 + V_2\).
Итак, мы получили объём тела R для обоих случаев. В случае а), когда тела P и Q не имеют общих внутренних точек, объём \(V_R = V_1 + V_2\). В случае б), когда объём общей части тел P и Q равен \(\frac{1}{3}V_1\), объём \(V_R = \frac{2}{3}V_1 + V_2\).
Ответы для обоих случаев совпадают с примером. Для случая а) объём \(V_R = V_1 + V_2\), и для случая б) объём \(V_R = \frac{2}{3}V_1 + V_2\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!