
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Исследовательские задачи Номер 4 Атанасян — Подробные Ответы
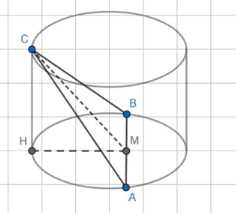
Найдите число попарно неравных друг другу равносторонних треугольников, все вершины которых принадлежат окружностям оснований цилиндра радиуса \(R\) с высотой \(h\).
1) В любом случае есть один треугольник, вписанный в основание такого цилиндра;
2) Рассмотрим равносторонний ΔАВС: \(CM \perp AB\), \(AM = BM = \frac{a}{2}\), \(
\(D = 9R^4 — 4R^2h^2 > 0, 9R^2 — 4h^2 \geq 0, R \geq \frac{2h}{3}\);
\(\alpha^2 = 2h^2 + 3R^2 — \sqrt{9R^4 — 4R^2h^2} \geq 0\);
\(2h^2 + 3R^2 \geq \sqrt{9R^4 — 4R^2h^2}, R \geq \frac{2h}{3}\);
\(4h^4 + 12h^2R^2 + 9R^4 \geq 9R^4 — 4R^2h^2\);
\(16h^2R^2 + 4h^4 \geq 0, 4R^2 + h^2 \geq 0\);
Ответ: при \(R < \frac{2h}{3}\) один треугольник;
при \(R = \frac{2h}{3}\) два треугольника;
при \(R > \frac{2h}{3}\) три треугольника.
Для решения задачи начнем с анализа данных о треугольниках, вписанных в цилиндр. Рассмотрим равносторонний треугольник \( \Delta ABC \), где \( CM \perp AB \), \( AM = BM = \frac{a}{2} \) и угол \( \angle CAB = 60^\circ \).
Согласно определению синуса, мы имеем:
\(\sin \angle CAB = \frac{CM}{AC} = \frac{a\sqrt{3}}{2}\).
Таким образом, высота \( CM \) равна:
\( CM = \frac{a\sqrt{3}}{2} \).
Теперь перейдем к равнобедренному треугольнику \( \Delta AHN \), где \( H \) — проекция точки \( C \) на ось \( AB \). Высота \( HM \) вычисляется по формуле:
\( HM = \sqrt{CM^2 — CH^2} = \sqrt{\frac{3a^2}{4} — h^2} = a\sqrt{3} — \frac{2h}{a} \).
Далее, для площади треугольника \( S_{\Delta AB} \) можно записать:
\(\frac{AB \cdot HM}{2S_{\Delta AB}} = \frac{a}{2} \cdot \frac{a\sqrt{3} — \frac{2h}{a}}{2} = \frac{a^2\sqrt{3}}{4} — \frac{h}{2}\).
Теперь найдем длину \( BH \) и \( AH \):
\( BH = AH = \sqrt{AM^2 + HM^2} = \sqrt{\frac{a^2}{4} + \left(a\sqrt{3} — \frac{2h}{a}\right)^2} = \frac{a}{2}\sqrt{3 — \left(\frac{2h}{a}\right)^2} \).
Теперь можем рассчитать радиус \( R \):
\( R = \frac{AH \cdot BH \cdot AB}{4S_{\Delta AB}} = \frac{(a^2 — h^2)\sqrt{3a^2 — 4h^2}}{4 \cdot \frac{a^2\sqrt{3}}{4}} = \frac{a^2 — h^2}{\sqrt{3a^2 — 4h^2}} \).
Теперь возведем \( R \) в квадрат:
\( R^2 = \frac{a^4 — 2a^2h^2 + h^4}{3a^2 — 4h^2} \).
Умножим обе стороны на \( 3a^2 — 4h^2 \):
\( 3a^2R^2 — 4R^2h^2 = a^4 — 2a^2h^2 + h^4 \).
Перепишем уравнение:
\( a^4 — (2h^2 + 3R^2)a^2 + h^4 + 4R^2h^2 = 0 \).
Теперь найдем дискриминант \( D \):
\( D = 4h^4 + 12R^2h^2 + 9R^4 — 4h^4 — 16R^2h^2 > 0 \).
Упрощая, получаем:
\( D = 9R^4 — 4R^2h^2 > 0 \).
Это приводит к неравенству:
\( 9R^2 — 4h^2 \geq 0 \) или \( R \geq \frac{2h}{3} \).
Теперь найдем выражение для \( \alpha^2 \):
\( \alpha^2 = 2h^2 + 3R^2 — \sqrt{9R^4 — 4R^2h^2} \geq 0 \).
Таким образом, мы получаем:
\( 2h^2 + 3R^2 \geq \sqrt{9R^4 — 4R^2h^2} \).
Теперь подставим это в неравенство:
\( 4h^4 + 12h^2R^2 + 9R^4 \geq 9R^4 — 4R^2h^2 \).
Упрощая, мы получаем:
\( 16h^2R^2 + 4h^4 \geq 0 \), что всегда верно, так как обе части неотрицательны.
Итак, мы приходим к следующему выводу: при \( R < \frac{2h}{3} \) существует один треугольник; при \( R = \frac{2h}{3} \) — два треугольника; при \( R > \frac{2h}{3} \) — три треугольника.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!