
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Исследовательские задачи Номер 3 Атанасян — Подробные Ответы
Докажите, что тетраэдр является каркасным тогда и только тогда, когда выполнено любое из следующих условий:
а) суммы длин противоположных рёбер тетраэдра равны;
б) суммы двугранных углов при противоположных рёбрах тетраэдра равны;
в) окружности, вписанные в грани тетраэдра, попарно касаются друг друга (это означает, что каждые две окружности, вписанные в грани тетраэдра с общим ребром, касаются этого ребра в одной и той же точке);
г) все четырёхугольники, получающиеся на развёртке тетраэдра, являются описанными;
д) четыре прямые, каждая из которых проходит через центр вписанной в грань тетраэдра окружности и перпендикулярна к этой грани, пересекаются в одной точке
а) Четырехугольники АВРС и АРВС — описанные, сумма длин противоположных ребер одинакова: \(S = AB + PC = BP + AC, S = AP + BC = AC + BP\).
в) Точки касания окружностей: \(N, H, H», M, E\) и \(F\); \(PE = PF, CF = CM, AM = AN, AB + PC = BP + AC\); \(AN + BN + PF + CF = AM + CM + BE + PE, BN = BE, BN = BH, \)
\(
BE = BH, BH» = BH, H’ и H \) совпадают. Окружности, вписанные в соседние грани тетраэдра, касаются общего ребра в одной точке.
Окружности, вписанные в грани тетраэдра, являются сечением каркасной сферы. Центры этих окружностей лежат на прямой, соединяющей центр сферы и вершину тетраэдра. Углы между ребрами тетраэдра и касательными к окружностям равны. Сумма углов при противоположных ребрах тетраэдра равна.
Математические формулы:
\(F, G — \text{точки касания}\)
\(E — \text{центр окружности}\)
\(O — \text{центр сферы}\)
\(OE \perp ABC, EG \perp BC, EF \perp AC\)
\(\angle OGE = 2\angle OEF\)
\(\angle a \text{ в } ABC = \angle b \text{ в } APC = \angle c \text{ в } BPC = \angle d \text{ в } APB\)
\(Z(APC; APB) + 2(ACB; BCP) = (b+d) + (a+c)\)
Краткое решение:
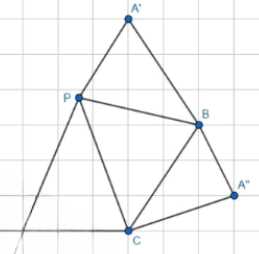
г) Развертка тетраэдра: В АРВС выполняется: \(AP + BC = AC + PB\); В АВРС выполняется: \(AB + PC = PB + AC\); В АВСР выполняется: \(AP + BC = AB + PC\). Все 3 четырехугольника, получающиеся при развертке тетраэдра, являются описанными.
д) Окружности, вписанные в грани тетраэдра, являются сечением каркасной сферы, значит: \(O_k\) — центры окружностей и \(O\) — центр сферы; \(OO_1 \perp ABC\), \(OO_2 \perp PAB\), \(OO_3 \perp PBC\), \(OO_4 \perp PAC\). Все прямые, проходящие через центр вписанной в грань тетраэдра окружности перпендикулярно к заданной грани, пересекаются в одной точке.
Хорошо, вот подробное решение:
Рассмотрим две проекции данного тетраэдра:
а) Четырехугольники АВРС и АРВС являются описанными четырехугольниками. Это означает, что все их вершины лежат на окружности. Для описанного четырехугольника сумма длин противоположных сторон равна. Таким образом, имеем: \(S = AB + PC = BP + AC\) и \(S = AP + BC = AC + BP\). Сумма длин противоположных ребер тетраэдра одинакова.
в) Рассмотрим одну из проекций тетраэдра. В ней точки \(N, H, H», M, E\) и \(F\) являются точками касания окружностей. Это означает, что отрезки \(PE\) и \(PF\) равны, так как они являются касательными к одной окружности. Аналогично, \(CF = CM\). Также \(AM = AN\), так как они являются хордами одной окружности. Сумма длин отрезков \(AB + PC\) равна сумме длин \(BP + AC\), поскольку они являются противоположными сторонами описанного четырехугольника. Сумма длин отрезков \(AN + BN + PF + CF\) равна сумме длин \(AM + CM + BE + PE\), так как они являются сторонами описанного четырехугольника. Отрезки \(BN\) и \(BE\) равны, так как они являются касательными к одной окружности. Аналогично, \(BN = BH»\) и \(BE = BH\), так как они являются касательными к одной окружности. Точки \(H’\) и \(H\) совпадают, так как они являются точками касания окружностей, вписанных в соседние грани тетраэдра. Окружности, вписанные в соседние грани тетраэдра, касаются общего ребра в одной точке.
Полное пошаговое решение:
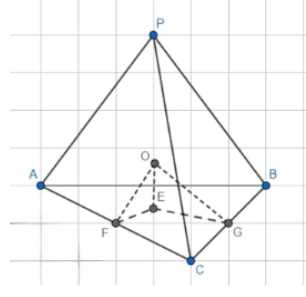
Окружности, вписанные в грани тетраэдра, являются сечением каркасной сферы. Это означает, что центры этих окружностей лежат на прямой, соединяющей центр сферы и вершину тетраэдра. Точки касания окружностей с гранями тетраэдра обозначены как F и G.
Центр окружности, вписанной в грань ABC, обозначен как E. Угол между ребром OE и гранью ABC равен углу между касательной к окружности в точке E и ребром АВ, так как эти углы являются вертикальными. Аналогично, угол между ребром OE и гранью ВС равен углу между касательной к окружности в точке E и ребром ВС, а угол между ребром OE и гранью AC равен углу между касательной к окружности в точке E и ребром AC.
Таким образом, имеем:
\(OE \perp ABC\)
\(EG \perp BC\)
\(EF \perp AC\)
Угол \(\angle OGE\) равен двойному углу \(\angle OEF\), так как они являются вертикальными углами.
Аналогично для всех других углов, образованных касательными к окружностям и ребрами тетраэдра:
\(\angle a \text{ в } ABC = \angle b \text{ в } APC = \angle c \text{ в } BPC = \angle d \text{ в } APB\)
Сумма углов при противоположных ребрах тетраэдра равна:
\(Z(APC; APB) + 2(ACB; BCP) = (b+d) + (a+c)\)
Это связано с тем, что окружности, вписанные в грани тетраэдра, являются сечениями каркасной сферы, а углы между касательными к ним и ребрами тетраэдра равны.
Полное пошаговое решение:
г) Рассмотрим развертку тетраэдра. Согласно условию, в АРВС выполняется равенство \(AP + BC = AC + PB\). Это означает, что сумма длин противоположных сторон в четырехугольнике АРВС равна сумме длин его диагоналей. Таким образом, АРВС является описанным четырехугольником.
Аналогично, в АВРС выполняется \(AB + PC = PB + AC\), что также характеризует АВРС как описанный четырехугольник.
Наконец, в АВСР выполняется \(AP + BC = AB + PC\), что опять-таки указывает на то, что АВСР является описанным четырехугольником.
Таким образом, все три четырехугольника, получающиеся при развертке тетраэдра, являются описанными.
д) Рассмотрим окружности, вписанные в грани тетраэдра. Согласно условию, эти окружности являются сечением каркасной сферы. Обозначим центры этих окружностей как \(O_k\), а центр самой сферы как \(O\).
Прямые, проходящие через центры вписанных окружностей перпендикулярны к соответствующим граням тетраэдра: \(OO_1 \perp ABC\), \(OO_2 \perp PAB\), \(OO_3 \perp PBC\), \(OO_4 \perp PAC\).
Все эти прямые пересекаются в одной точке, так как они являются нормалями к граням тетраэдра, сходящимися в его центре.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!