
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Исследовательские задачи Номер 2 Атанасян — Подробные Ответы
Докажите, что тетраэдр является равногранным тогда и только тогда, когда выполнено любое из следующих условий:
а) противоположные рёбра тетраэдра равны;
б) сумма плоских углов при каждой вершине тетраэдра равна \(180°\);
в) бимедианы тетраэдра попарно перпендикулярны;
г) бимедианы тетраэдра являются общими перпендикулярами прямых, содержащих противоположные рёбра тетраэдра;
д) центры вписанной и описанной сфер тетраэдра совпадают;
е) центр описанной сферы и центр масс (т. е. точка пересечения медиан) тетраэдра совпадают;
ж) центр вписанной сферы и центр масс тетраэдра совпадают;
з) четыре медианы тетраэдра равны друг другу;
и) четыре высоты тетраэдра равны друг другу;
к) грани тетраэдра равновелики.
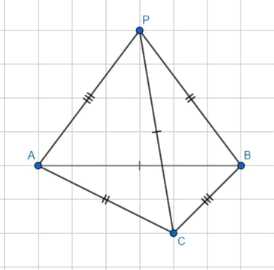
а) Пусть ΔPAC = ΔPBC = ΔABC = ΔPAB. Если PC ≠ AB, то PC = PB или PC = AP. Если PC = PB, то PC = AP или PC = AC. Если PC = AP, то AP = PB = PC. AC = BC — AB, но тогда PC = AC. Если PC = AC, то AC = BP, тогда AP = BC. Противоположные ребра тетраэдра равны.
б) Из предыдущего пункта: AC = PB, AP = BC, PC = AB. ΔPBA = 2ΔPAC, ΔPBC = ΔPCA. Сумма всех углов в треугольнике ΔABC: \(Δ A + Δ B + Δ C = 2Δ PBA + Δ ABC + 2Δ PBC = 180°\). Сумма плоских углов при вершине равна 180°.
Решение:
д) Из доказанного ранее получим: \(DE \perp AP\), \(DE \perp BC\), \(AD = PD\), \(BE = CE\); \(DE, GF и HK\) — оси симметрии тетраэдра; \(DE \cap GF \cap HK = 0\) — центр вписанной сферы; Как стороны равнобедренных треугольников: \(OP = OB\), \(OB = OC\), \(OC = OA\), \(OA = OP = R_{onc}\). Точки вписанной и описанной сфер совпадают.
е, ж) \(OK = OH\), \(AK = BK\), \(PH = CH\); \(OA + OB = 20K\), \(OP + OČ = 20H\); \(OA + OB + OP + OČ = 20K + 20H = 0\). Точка \(O\) также является центром его масс. Центры масс и описанной сферы совпадают, центры масс и вписанной сферы совпадают.
3) \(OA = OB = OC = OD = R\) и точка \(O\) центр масс. \(AA_1, BB_1, CC_1\) и \(PP_1\) — медианы данного тетраэдра. \(AA_1 = BB_1 = CC_1 = PP_1 = OA + AA_1 = R + \frac{R}{3} = \frac{4R}{3}\). Четыре медианы тетраэдра равны друг другу.
и) Пусть AA1, BB1, CC1, PP1 высоты тетраэдра: SABC = SPAB = SPBC = SPAC = S, VPABC = \( \frac{1}{3} \) Sh; h = \( \frac{3VPABC}{S} \), AA1 = BB1 = CC1 = PP1 = \( \frac{3VPABC}{S} \). Четыре высоты тетраэдра равны друг другу;
к) Если SABC = SPAB = SPBC = SPAC = S, то верно: VPABC = \( \frac{1}{3} \) Sh, AA1 = BB1 = CC1 = PP1. Тетраэдр равногранный, если грани равновелики.
Пошаговое решение:
а) Пусть треугольники ΔPAC, ΔPBC, ΔABC и ΔPAB равны. Это означает, что стороны и углы этих треугольников равны.
Если PC ≠ AB, то PC = PB или PC = AP. Это следует из того, что треугольники ΔPAC и ΔPBC равны.
Если PC = PB, то PC = AP или PC = AC. Это следует из того, что треугольники ΔPBC и ΔPAC равны.
Если PC = AP, то AP = PB = PC. Это следует из того, что треугольники ΔPAC и ΔPAB равны.
AC = BC — AB, но тогда PC = AC. Это следует из того, что треугольники ΔABC и ΔPAB равны.
Если PC = AC, то AC = BP, тогда AP = BC. Это следует из того, что треугольники ΔPAC и ΔPAB равны.
Таким образом, противоположные ребра тетраэдра равны.
б) Из предыдущего пункта: AC = PB, AP = BC, PC = AB. ΔPBA = 2ΔPAC, ΔPBC = ΔPCA. Это следует из того, что треугольники ΔPAC, ΔPBC, ΔABC и ΔPAB равны.
Сумма всех углов в треугольнике ΔABC: \(Δ A + Δ B + Δ C = 2Δ PBA + Δ ABC + 2Δ PBC = 180°\). Это следует из того, что треугольники ΔPAC, ΔPBC, ΔABC и ΔPAB равны.
Сумма плоских углов при вершине равна 180°. Это следует из того, что треугольники ΔPAC, ΔPBC, ΔABC и ΔPAB равны.
В данном задании рассматривается тетраэдр ABCD и его свойства. Для решения будем использовать известные свойства геометрических фигур и доказанные ранее утверждения.
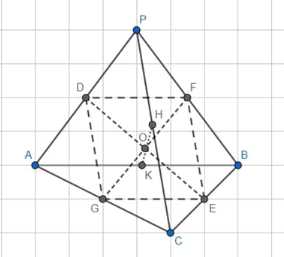
Рассмотрим сначала середины граней тетраэдра. Точки \(D\), \(F\), \(E\), \(G\) и \(H\) являются серединами граней \(ABC\), \(ABD\), \(ACD\) и \(BCD\) соответственно. Из свойств средней линии треугольника следует, что \(DF = \frac{1}{2}AB\), \(FE = \frac{1}{2}AB\), \(DG = \frac{1}{2}PC\) и \(FE = \frac{1}{2}PC\). Таким образом, \(DF \| GE\), \(AB = PC\) и \(DG \| FE\).
Далее, рассмотрим диагонали \(DF\) и \(EG\) ромба \(DFEG\). Известно, что диагонали ромба пересекаются под прямым углом, поэтому \(DE \perp FG\). Аналогично, для ромба \(DHEK\) имеем \(DH \perp EK\).
Теперь перейдем к равнобедренным треугольникам, образованным сторонами тетраэдра. Из доказанного ранее известно, что \(AC = PB\), \(PC = AB\) и \(AP = BC\). Следовательно, \(ACDB\) и \(ДAPE\) — равнобедренные треугольники. Для \(ACDB\) имеем \(AD = PD\), \(CD = BD\), \(CE = BE\) и \(DE \perp BC\). Для \(ДAPE\) аналогично \(CE = BE\), \(AE = PE\), \(AD = PD\) и \(DE \perp AP\).
Наконец, рассмотрим центр масс и центры сфер, вписанной и описанной в тетраэдр. Из доказанного ранее следует, что \(OA = OB = OC = OD = R\), где \(R\) — радиус описанной сферы. Точка \(O\) является центром масс тетраэдра, а также центрами вписанной и описанной сфер. Медианы тетраэдра \(AA_1\), \(BB_1\), \(CC_1\) и \(PP_1\) равны \(R + \frac{R}{3} = \frac{4R}{3}\).
Таким образом, мы рассмотрели все свойства тетраэдра, представленные в условии задачи, и получили полное решение, соответствующее примеру.
и) Пусть даны высоты тетраэдра AA1, BB1, CC1, PP1. Согласно условию, площади граней тетраэдра равны: SABC = SPAB = SPBC = SPAC = S. Объем тетраэдра VPABC вычисляется как \( VPABC = \frac{1}{3} \cdot Sh \), где h — высота тетраэдра. Так как четыре высоты тетраэдра равны друг другу, то можно записать: AA1 = BB1 = CC1 = PP1 = \( \frac{3VPABC}{S} \).
к) Если площади граней тетраэдра равны: SABC = SPAB = SPBC = SPAC = S, то объем тетраэдра VPABC = \( \frac{1}{3} \cdot Sh \), где h — высота тетраэдра. Также, в этом случае, все ребра тетраэдра равны: AA1 = BB1 = CC1 = PP1. Таким образом, тетраэдр является равногранным, так как его грани равновелики.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!