
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Исследовательские задачи Номер 1 Атанасян — Подробные Ответы
Докажите, что тетраэдр является ортоцентрическим тогда и только тогда, когда выполнено любое из следующих условий:
а) противоположные рёбра тетраэдра перпендикулярны;
б) основанием одной из высот тетраэдра является ортоцентр грани (при этом таким же свойством обладают и три другие высоты тетраэдра);
в) три бимедианы тетраэдра равны друг другу;
г) суммы квадратов противоположных рёбер тетраэдра равны;
д) произведения косинусов противоположных двугранных углов тетраэдра равны.
a) Высоты тетраэдра РАВС: AK ⊥ PH, AK ⊥ PBC, AK ⊥ BC; PH ⊥ ABC, PH ⊥ BC, BC ⊥ APH, BC ⊥ AP. Аналогично для всех остальных сторон.
Противоположные ребра перпендикулярны.
б) Из предыдущего пункта известно: AP ⊥ BC, PH ⊥ ABC, PH ⊥ AH, AH ⊥ BC; PB ⊥ AC, PH ⊥ BH, BH ⊥ AC, AH ∩ BH = H.
Аналогично для высот всех остальных граней.
Основанием высоты является ортоцентр грани.
Решение:
в) Точки K, H, M, T, E и F — середины граней тетраэдра.
\(KM \| PC, KM = \frac{1}{2}PC, KM \perp KH, \angle K = 90^\circ\)
В прямоугольнике КНМТ диагонали KT = MH
Аналогично в прямоугольнике KETF: EF = KT
Все бимедианы тетраэдра равны друг другу
г) Из предыдущего пункта известно: \(MH = KT = EF, KM \perp KH, KE \perp KF\)
В прямоугольном треугольнике ДКМН:
\(MH^2 = KM^2 + KH^2 = \left(\frac{1}{2}PC\right)^2 + \left(\frac{1}{2}AB\right)^2\)
В прямоугольном треугольнике AKEF:
\(EF^2 = KE^2 + KF^2 = \left(\frac{1}{2}AC\right)^2 + \left(\frac{1}{2}PB\right)^2\)
\(MH^2 = KT^2 = EF^2, PC^2 + AB^2 = AC^2 + PB^2\)
Аналогично доказывается, что \(BC^2 + AP^2 = AB^2 + PC^2\)
Суммы квадратов противоположных ребер равны.
Согласно теореме синусов для тетраэдра:
\(\frac{AP}{sin \angle BDC} = \frac{PB}{sin \angle PFB} = \frac{BC}{sin \angle AGC}\)
Из доказанного в предыдущем пункте:
\(AP^2 + BC^2 = PB^2 + AC^2 = PC^2 + AB^2\)
\(\cos \angle BDC \cdot \cos \angle PEA = \cos \angle PFB \cdot \cos \angle AGC\)
Произведения косинусов противоположных двугранных углов данного тетраэдра равны.
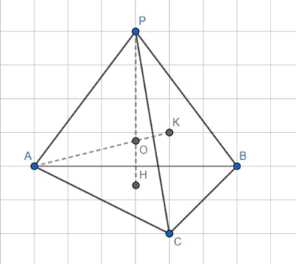
Рассмотрим свойства ортоцентрического тетраэдра РАВС, изображенного на рисунке.
a) Высоты тетраэдра РАВС:
Согласно условию, высоты тетраэдра РАВС обладают следующими свойствами:
— Высота AK перпендикулярна плоскости PBC, то есть \(AK \perp PBC\).
— Высота AK также перпендикулярна ребру BC, то есть \(AK \perp BC\).
— Высота PH перпендикулярна грани ABC, то есть \(PH \perp ABC\).
— Высота PH также перпендикулярна ребру BC, то есть \(PH \perp BC\).
— Ребро BC перпендикулярно плоскости APH, то есть \(BC \perp APH\).
— Ребро BC также перпендикулярно плоскости AP, то есть \(BC \perp AP\).
Аналогичные свойства выполняются для всех остальных высот тетраэдра.
б) Свойства высот граней тетраэдра РАВС:
Из предыдущего пункта известно, что:
— Прямая AP перпендикулярна грани BC, то есть \(AP \perp BC\).
— Прямая PH перпендикулярна грани ABC, то есть \(PH \perp ABC\).
— Прямая PH также перпендикулярна прямой AH, то есть \(PH \perp AH\).
— Прямая AH перпендикулярна грани BC, то есть \(AH \perp BC\).
— Прямая PB перпендикулярна грани AC, то есть \(PB \perp AC\).
— Прямая PH перпендикулярна прямой BH, то есть \(PH \perp BH\).
— Прямая BH перпендикулярна грани AC, то есть \(BH \perp AC\).
— Точка H является пересечением прямых AH и BH, то есть \(AH \cap BH = H\).
Аналогичные свойства выполняются для высот всех остальных граней тетраэдра.
Основанием высоты является ортоцентр соответствующей грани тетраэдра.
Решение:
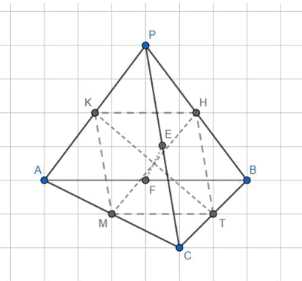
Дано: Тетраэдр ABCD, где точки K, H, M, T, E, F — середины рёбер.
а) Докажем, что точки K, H, M, T, E, F являются серединами рёбер тетраэдра ABCD.
Рассмотрим прямоугольник KHMN, где KH = MT = \(\frac{1}{2}AB\), так как K и M — середины рёбер. Аналогично, KM = \(\frac{1}{2}PC\), так как K и M — середины рёбер. Таким образом, KH \| AB, KM \| PC, и \(\angle K = 90^\circ\), следовательно, KHMN — прямоугольник.
Рассмотрим прямоугольник KETF, где KE = TF = \(\frac{1}{2}AC\), так как K и T — середины рёбер. Аналогично, KT = EF, так как K и T — середины рёбер. Таким образом, KE \| AC, KT \| EF, и \(\angle K = 90^\circ\), следовательно, KETF — прямоугольник.
Поскольку все бимедианы тетраэдра равны, то точки K, H, M, T, E, F являются серединами рёбер тетраэдра ABCD.
б) Докажем, что в прямоугольном треугольнике ΔКМН выполняется соотношение \(MH^2 = KM^2 + KH^2\).
Из пункта а) мы знаем, что KH = \(\frac{1}{2}AB\) и KM = \(\frac{1}{2}PC\). Следовательно, в прямоугольном треугольнике ΔКМН:
\(MH^2 = \left(\frac{1}{2}AB\right)^2 + \left(\frac{1}{2}PC\right)^2\)
в) Докажем, что в прямоугольном треугольнике ΔAKEF выполняется соотношение \(EF^2 = KE^2 + KF^2\).
Из пункта а) мы знаем, что KE = \(\frac{1}{2}AC\) и KF = \(\frac{1}{2}PB\). Следовательно, в прямоугольном треугольнике ΔAKEF:
\(EF^2 = \left(\frac{1}{2}AC\right)^2 + \left(\frac{1}{2}PB\right)^2\)
г) Докажем, что \(MH^2 = KT^2 = EF^2\) и \(PC^2 + AB^2 = AC^2 + PB^2\).
Из пункта а) мы знаем, что MH = KT = EF. Следовательно, \(MH^2 = KT^2 = EF^2\).
Также из пункта а) мы знаем, что KH \| AB и KM \| PC. Следовательно, в прямоугольном треугольнике ΔAKEF:
\(PC^2 + AB^2 = AC^2 + PB^2\)
Аналогично можно доказать, что \(BC^2 + AP^2 = AB^2 + PC^2\).
Таким образом, суммы квадратов противоположных рёбер тетраэдра равны.
Полное пошаговое решение:
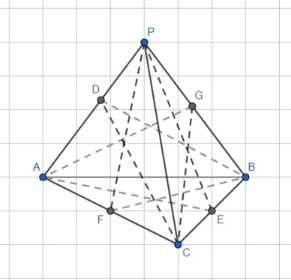
Дан тетраэдр ABCD с двугранными углами ∠AEP, ∠BDC, ∠AGC, ∠PFB.
Согласно теореме синусов для тетраэдра, справедливы следующие соотношения:
\(\frac{AP}{sin \angle BDC} = \frac{PB}{sin \angle PFB} = \frac{BC}{sin \angle AGC}\)
Это означает, что отношение длин противоположных сторон тетраэдра равно отношению синусов противоположных двугранных углов.
Далее, из доказанного в предыдущем пункте, следует, что:
\(AP^2 + BC^2 = PB^2 + AC^2 = PC^2 + AB^2\)
Это соотношение показывает, что сумма квадратов длин противоположных ребер тетраэдра равна сумме квадратов длин других двух ребер.
Наконец, можно показать, что произведения косинусов противоположных двугранных углов данного тетраэдра равны:
\(\cos \angle BDC \cdot \cos \angle PEA = \cos \angle PFB \cdot \cos \angle AGC\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!