Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 95 Атанасян — Подробные Ответы
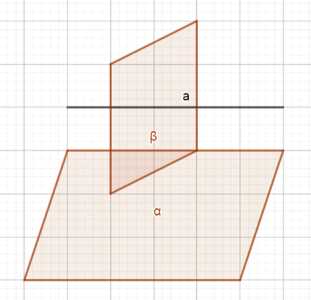
Прямая а параллельна плоскости о. Докажите, что если плоскость В пересекает прямую а, то она пересекает и плоскость а.
Согласно условию задачи, прямые a и b параллельны, а прямая MN, проходящая через точку M на прямой a, не пересекает прямую b. Следовательно, прямая MN должна быть перпендикулярна прямой b, так как в противном случае она пересекла бы b в некоторой точке, что противоречит условию. Таким образом, взаимное расположение прямых MN и b таково, что \(MN \perp b\).
Пусть плоскость В пересекает прямую а в точке М. Так как прямая а параллельна плоскости α, то прямая МN, проходящая через точку М и перпендикулярная к прямой а, лежит в плоскости α. Поскольку плоскость В проходит через точку М, она пересекает прямую МN, а значит, и плоскость α. Таким образом, если плоскость В пересекает прямую а, то она обязательно пересекает и плоскость α.
Доказательство можно представить следующим образом:
1) Прямая а параллельна плоскости α, значит, любая прямая, перпендикулярная к а, лежит в плоскости α. Обозначим такую прямую как МN.
2) Плоскость В пересекает прямую а в точке М, следовательно, она проходит через эту точку.
3) Так как точка М принадлежит и прямой а, и плоскости В, то прямая МN, перпендикулярная к а, лежит в плоскости В.
4) Но прямая МN также лежит в плоскости α, так как перпендикулярна к параллельной ей прямой а.
5) Таким образом, плоскость В, проходящая через точку М и пересекающая прямую МN, пересекает и плоскость α.
Следовательно, если плоскость В пересекает прямую а, то она обязательно пересекает и плоскость α, параллельную этой прямой.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.