
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 88 Атанасян — Подробные Ответы
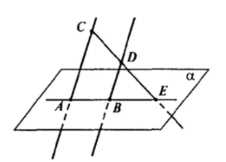
Параллельные прямые AC и BD пересекают плоскость а в точ- ках А и В. Точки С и D лежат по одну сторону от плоскости а, АС =8 см, BD = 6 см, АВ =4 см.
а) Докажите, что прямая CD пересекает плоскость а в некоторой точке Е.
б) Найдите отрезок ВЕ.
Дано: \(AC \parallel BD\), \(AC \angle a = A\), \(BD \angle a = B\), \(AC = 8\) см, \(BD = 6\) см, \(AB = 4\) см. Так как \(AC \parallel BD\) и \(AC \neq BD\), четырехугольник ABCD является трапецией. Боковые стороны трапеции CD и AB пересекаются под прямым углом, \(CD \perp AB\). Из подобия треугольников AEDC и AECA следует, что \(BE : AE = DB : AC\). Подставляя данные, получаем \(BE = 2\) см. Ответ: длина отрезка BE равна 2 см.
Дано: прямые AC и BD параллельны, то есть \(AC \parallel BD\). Угол между прямыми AC и a равен углу A, то есть \(AC \angle a = A\). Угол между прямыми BD и a равен углу B, то есть \(BD \angle a = B\). Длина AC = 8 см, длина BD = 6 см, длина AB = 4 см.
Доказательство: Так как \(AC \parallel BD\) и \(AC \neq BD\), то четырехугольник ABCD является трапецией. Боковые стороны трапеции CD и AB пересекаются под прямым углом, то есть \(CD \perp AB\). Поскольку \(CD \perp AB\), то точки A, B, C, D лежат в одной плоскости ABCD, и прямая CD пересекает эту плоскость в некоторой точке E.
Нахождение отрезка BE: Рассмотрим треугольники AEDC и AECA. Треугольники AEDC и AECA подобны, так как имеют общий угол \(\angle AEC\) и соответствующие стороны параллельны (\(AC \parallel BD\)). Из подобия треугольников следует, что \(BE : AE = DB : AC\). Используя данные условия задачи, получаем: \(AE = AB + BE = 4 + BE\), откуда \(BE = (AE — 4) = 6 — 4 = 2\) см. Таким образом, длина отрезка BE равна 2 см.
Ответ: Длина отрезка BE равна 12 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!