
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 87 Атанасян — Подробные Ответы
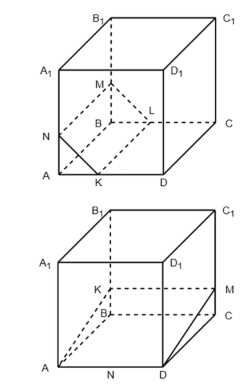
Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью MNK, где точки М, N и K лежат соответственно на рёбрах: а) ВВ1, АА1, AD; б) CC1, AD, ВВ1.
Для построения сечения параллелепипеда плоскостью, проходящей через точки \(M\), \(N\) и \(K\), расположенные на ребрах \(BB_1\), \(AA_1\) и \(AD\) соответственно, необходимо: 1) изобразить параллелепипед \(ABCDA_1B_1C_1D_1\); 2) отметить точки \(M\), \(N\) и \(K\) на соответствующих ребрах; 3) соединить точки \(N\) и \(K\); 4) провести линию, параллельную \(NK\), через точку \(M\), пересекающую сторону \(C_1CBB_1\) в точке \(P\); 5) соединить точки \(M\), \(N\), \(K\) и \(P\), получив сечение параллелепипеда плоскостью \(MNK\). Для построения сечения плоскостью, проходящей через точки \(M\), \(N\) и \(K\), расположенные на ребрах \(CC_1\), \(DA\) и \(BB_1\) соответственно, необходимо: 1) изобразить параллелепипед \(ABCDA_1B_1C_1D_1\); 2) отметить точки \(M\), \(N\) и \(K\) на соответствующих ребрах; 3) соединить точки \(M\) и \(K\); 4) провести линию, параллельную \(MK\), через точку \(N\), пересекающую сторону \(DD_1AA_1\) в точке \(P\); 5) провести линию, параллельную \(PK\), через точку \(M\), пересекающую сторону \(D_1DCC_1\) в точке \(Q\); 6) соединить точки \(M\), \(N\), \(K\), \(P\) и \(Q\), получив сечение параллелепипеда плоскостью \(MNKPQ\).
a) Для построения сечения параллелепипеда плоскостью, проходящей через точки M, N и K, расположенные соответственно на ребрах BB1, AA1 и AD, выполним следующие действия:
1. Изобразим параллелепипед ABCDA1B1C1D1.
2. Отметим случайно точки M, N и K на соответствующих ребрах.
3. Соединим точки N и K, так как они лежат на одной стороне параллелепипеда.
4. Проведем линию, параллельную NK, через точку M. Эта линия пересечет сторону C1CBB1 в точке P.
5. Соединим точки M, N, K и P, получив сечение параллелепипеда плоскостью MNK.
б) Для построения сечения параллелепипеда плоскостью, проходящей через точки M, N и K, расположенные соответственно на ребрах CC1, DA и BB1, выполним следующие действия:
1. Изобразим параллелепипед ABCDA1B1C1D1.
2. Отметим случайно точки M, N и K на соответствующих ребрах.
3. Соединим точки M и K, так как они лежат на одной стороне параллелепипеда.
4. Проведем линию, параллельную MK, через точку N. Эта линия пересечет сторону DD1AA1 в точке P.
5. Проведем линию, параллельную PK, через точку M. Эта линия пересечет сторону D1DCC1 в точке Q.
6. Соединим точки M, N, K, P и Q, получив сечение параллелепипеда плоскостью MNKPQ.
Таким образом, мы построили сечения параллелепипеда плоскостями, проходящими через заданные точки на его ребрах.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!