
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 86 Атанасян — Подробные Ответы
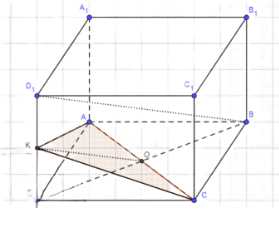
Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через диагональ AC основания параллельно диагонали BD1. Докажите, что если основание параллелепипеда — ромб и углы ABB1 и CBB1 прямые, то построенное сечение — равнобедренный треугольник.
Дано: параллелепипед ABCDA1B1C1D1, где основание ABCD — ромб, а углы ABB1 и CBB1 прямые. Доказать, что сечение параллелепипеда плоскостью, проходящей через диагональ AC основания параллельно диагонали BD1, является равнобедренным треугольником.
Доказательство: Так как плоскость сечения проходит через диагональ AC, она проходит и через точку O — пересечение диагоналей ABCD. Поскольку AC \(\perp\) BD1 (так как ABCD — ромб), плоскость сечения также \(\perp\) BD1. Пусть плоскость сечения пересекает BD1 в точке M, тогда \(a \cap BD1 = m\), где \(a\) — плоскость сечения, и \(m\) — отрезок, на который она делит BD1. Рассмотрим треугольник ABDD1: так как OM \(\perp\) BD1 и O — середина BD, то MO является средней линией треугольника ABDD1, следовательно, K — середина DD1. Точки A и K принадлежат плоскости сечения ADD1, поэтому \(AK = a \cap ADD1\), аналогично, \(KC = a \cap CDD1\). Таким образом, сечение параллелепипеда является треугольником АКС. Так как ABCDA1B1C1D1 — параллелепипед, то \(\angle ADD1 = \angle CDD1 = 90^\circ\). Рассмотрим прямоугольные треугольники AMD и CMD: \(\angle AMD = \angle CMD = 90^\circ\), \(AD = DC\) (так как ABCD — ромб), и MD — общая сторона, следовательно, \(\triangle AMD \cong \triangle CMD\), и \(AK = KC\). Таким образом, треугольник АКС является равнобедренным.
Дано: параллелепипед ABCDA1B1C1D1, где основание ABCD — ромб, а углы ABB1 и CBB1 прямые.
Доказательство:
Рассмотрим сечение параллелепипеда плоскостью, проходящей через диагональ AC основания параллельно диагонали BD1.
1. Так как плоскость сечения проходит через диагональ AC, то она проходит и через точку O — точку пересечения диагоналей ABCD.
2. Поскольку AC пересекает BD1 под прямым углом (так как ABCD — ромб), то плоскость сечения также пересекает BD1 под прямым углом.
3. Пусть плоскость сечения пересекает BD1 в точке M, тогда \(a \cap BD1 = m\), где \(a\) — плоскость сечения, и \(m\) — отрезок, на который она делит BD1.
4. Рассмотрим треугольник ABDD1:
— Так как OM \(\perp\) BD1 и O — середина BD, то MO является средней линией треугольника ABDD1.
— Следовательно, K — середина DD1.
5. Точки A и K принадлежат плоскости сечения ADD1, поэтому \(AK = a \cap ADD1\).
6. Аналогично, точки C и K принадлежат плоскости сечения CDD1, поэтому \(KC = a \cap CDD1\).
7. Таким образом, сечение параллелепипеда является треугольником АКС.
8. Так как ABCDA1B1C1D1 — параллелепипед, то \(\angle ADD1 = \angle CDD1 = 90^\circ\).
9. Рассмотрим прямоугольные треугольники AMD и CMD:
— \(\angle AMD = \angle CMD = 90^\circ\)
— \(AD = DC\) (так как ABCD — ромб)
— MD — общая сторона
— Следовательно, \(\triangle AMD \cong \triangle CMD\), и \(AK = KC\).
10. Таким образом, треугольник АКС является равнобедренным, что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!