
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 8 Атанасян — Подробные Ответы
Верно ли утверждение: а) если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости; б) если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости?
а) Если две точки окружности лежат в плоскости, это не гарантирует, что вся окружность лежит в этой плоскости, так как окружность может быть наклонена. Утверждение неверно.
б) Если три точки окружности лежат в плоскости, то вся окружность также лежит в этой плоскости, так как через три точки, не лежащие на одной прямой, проходит единственная плоскость. Утверждение верно.
Утверждение:
а) Если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости.
б) Если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости.
Рассмотрим каждое утверждение по отдельности.
Для пункта а):
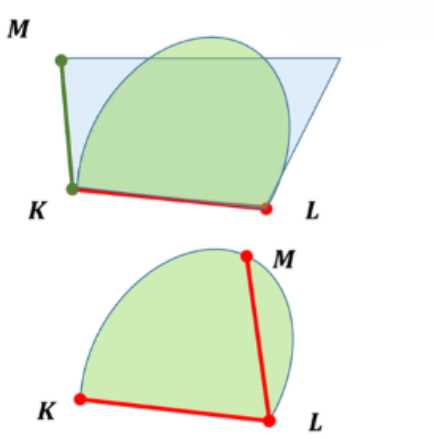
Пусть даны две точки \(K\) и \(L\), принадлежащие окружности \(c\), и известно, что \(K, L \in \beta\), где \(\beta\) — некоторая плоскость.
Окружность \(c\) определяется как множество всех точек, равноудалённых от её центра \(O\). Если известно только, что две точки окружности \(K\) и \(L\) лежат в плоскости \(\beta\), это не гарантирует, что центр \(O\) также лежит в этой плоскости. Следовательно, окружность \(c\) может быть наклонена относительно плоскости \(\beta\), и не вся окружность будет принадлежать этой плоскости.
Пример: если окружность расположена в пространстве так, что её плоскость не совпадает с \(\beta\), то хорда \(KL\) может лежать в \(\beta\), но сама окружность — нет.
Таким образом, утверждение а) неверно.
Для пункта б):
Пусть даны три точки \(K, L, M\), принадлежащие окружности \(c\), и известно, что \(K, L, M \in \beta\), где \(\beta\) — некоторая плоскость.
Через три точки, не лежащие на одной прямой, можно провести единственную плоскость (аксиома о трёх точках). Так как точки \(K, L, M\) принадлежат окружности \(c\) и одновременно лежат в плоскости \(\beta\), то вся окружность \(c\) также лежит в плоскости \(\beta\). Это связано с тем, что окружность определяется как множество точек, равноудалённых от центра \(O\), и её плоскость однозначно задаётся любыми тремя её точками, не лежащими на одной прямой.
Следовательно, утверждение б) верно.
Ответ:
а) Неверно.
б) Верно.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!