ГДЗ по Геометрии 10 класс Номер 79 Атанасян — Подробные Ответы
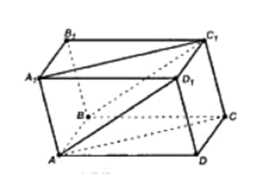
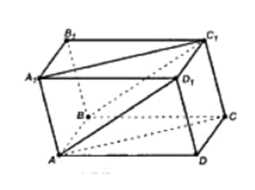
Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение: а) плоскостью ABC1; б) плоскостью ACC1. Докажите, что построенные сечения являются параллелограммами.
Рассмотрим сечение параллелепипеда ABCDA1B1C1D1 плоскостью ABC1. Плоскость BB1C,C параллельна плоскости AA1D,D1 по свойству параллелепипеда, следовательно, прямая BC1 параллельна прямой AA1. Точка А является общей для плоскостей ABC1 и AA1D1, поэтому сечение ABC1 пересекается с плоскостью AA1D1 по прямой, проходящей через точку А и параллельной ВС1, то есть по прямой AD. Таким образом, сечение ABC1 является четырехугольником ABC1D1, который является параллелограммом, так как его противоположные стороны параллельны и равны \((AB = CD, BC1 = AD)\).
Рассмотрим сечение параллелепипеда ABCDA1B1C1D1 плоскостью ACC1. Плоскости граней B1C1CB и AD,DA пересечены плоскостью ACC1, линии пересечения этих плоскостей параллельны, так как они параллельны ребрам параллелепипеда \((AA1 || CC1)\). Следовательно, сечение ACC1 является параллелограммом, так как его противоположные стороны параллельны и равны \((AC = C1A1, CA1 = AC1)\).
Рассмотрим сечение параллелепипеда ABCDA1B1C1D1 плоскостью ABC1:
1. Плоскость BB1C,C параллельна плоскости AA1D,D1 по свойству параллелепипеда. Следовательно, прямая BC1 параллельна прямой AA1.
2. Точка А является общей для плоскостей ABC1 и AA1D1, поэтому сечение ABC1 пересекается с плоскостью AA1D1 по прямой, проходящей через точку А и параллельной ВС1, то есть по прямой AD.
3. Таким образом, сечение ABC1 является четырехугольником ABC1D1, который является параллелограммом, так как его противоположные стороны параллельны и равны (AB = CD, BC1 = AD).
Рассмотрим сечение параллелепипеда ABCDA1B1C1D1 плоскостью ACC1:
1. Плоскости граней B1C1CB и AD,DA пересечены плоскостью ACC1.
2. Линии пересечения этих плоскостей параллельны, так как они параллельны ребрам параллелепипеда (AA1 || CC1).
3. Следовательно, сечение ACC1 является параллелограммом, так как его противоположные стороны параллельны и равны (AC = C1A1, CA1 = AC1).
Таким образом, оба построенных сечения являются параллелограммами.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.
Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!