
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 75 Атанасян — Подробные Ответы
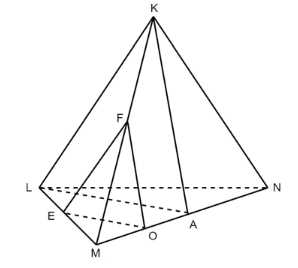
Изобразите тетраэдр KLMN. а) Постройте сечение этого тетраэдра плоскостью, проходящей через ребро KL и середину А ребра MN. б) Докажите, что плоскость, проходящая через середины Е, О и F, отрезков LM, МА и МK, параллельна плоскости LKA. Найдите площадь треугольника EOF, если площадь треугольника LKA равна 24 см2.
Согласно условию, средние линии EOF и KLA параллельны соответствующим сторонам тетраэдра KLMN. Это означает, что плоскость, проходящая через середины E, O и F, параллельна плоскости LKA. Используя подобие треугольников EOF и KLA, можно найти площадь треугольника EOF: \(S_{\text{EOF}} = \frac{1}{4} S_{\text{KLA}}\), где \(S_{\text{KLA}} = 24 \text{ см}^2\). Таким образом, \(S_{\text{EOF}} = \frac{1}{4} \cdot 24 = 6 \text{ см}^2\).
Пусть тетраэдр KLMN изображен на рисунке. Для решения задачи нам необходимо построить сечение тетраэдра плоскостью, проходящей через ребро KL и середину A ребра MN, а также найти площадь треугольника EOF.
а) Построение сечения тетраэдра KLMN плоскостью, проходящей через ребро KL и середину A ребра MN:
Плоскость, проходящая через ребро KL и середину A ребра MN, является средней плоскостью тетраэдра KLMN. Эта плоскость пересекает тетраэдр по треугольнику KAL, который является сечением тетраэдра.
б) Доказательство, что плоскость, проходящая через середины E, O и F, параллельна плоскости LKA:
Согласно условию, средние линии EOF и KLA параллельны соответствующим сторонам тетраэдра. Это означает, что плоскость, проходящая через середины E, O и F, параллельна плоскости LKA.
Для нахождения площади треугольника EOF, используем подобие треугольников EOF и KLA:
\(S_{\text{EOF}} = \frac{1}{4} S_{\text{KLA}}\)
Поскольку \(S_{\text{KLA}} = 24 \text{ см}^2\), то
\(S_{\text{EOF}} = \frac{1}{4} \cdot 24 = 6 \text{ см}^2\)
Таким образом, площадь треугольника EOF равна \(6 \text{ см}^2\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!