ГДЗ по Геометрии 10 класс Номер 74 Атанасян — Подробные Ответы

Через точку пересечения медиан грани \(BCD\) тетраэдра \(ABCD\) про- ведена плоскость, параллельная грани \(АВС\).
а) Докажите, что сечение тетраэдра этой плоскостью есть треуголь- ник, подобный треугольнику \(АВС\).
б) Найдите отношение площадей сечения и треугольника \(АВС\).

а) Докажем подобие треугольников \(ABC\) и \(PRQ\): \(\frac{DP}{DA} = \frac{DQ}{DC} = \frac{DR}{DB} = k\), где \(k = \frac{2}{3}\), так как точка \(O\) делит медианы в отношении \(1:2\). Следовательно, треугольники \(ABC\) и \(PRQ\) подобны.

б) Отношение площадей треугольников \(ABC\) и \(PRQ\) вычисляется по формуле: \(\frac{S_{PRQ}}{S_{ABC}} = \frac{PR \cdot PQ \cdot \sin \angle RPQ}{AB \cdot AC \cdot \sin \angle BAC} = \frac{1}{k^2} = \frac{9}{4}\).

а) Докажем, что сечение тетраэдра плоскостью, параллельной грани \(ABC\), является треугольником, подобным треугольнику \(ABC\).

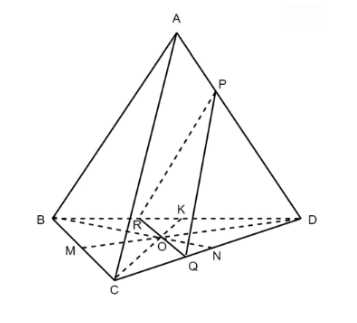
Рассмотрим медианы \(DM\), \(BN\) и \(CK\) грани \(BCD\) тетраэдра \(ABCD\). Точка пересечения этих медиан обозначим как \(O\). Проведем прямую \(RQ\) параллельно ребру \(BC\) через точку \(O\). Также проведем прямую \(PQ\) параллельно ребру \(AC\) через точку \(Q\).

По признаку параллельности плоскостей, плоскость \(ABC\) параллельна плоскости \(PRQ\). Соединим точки \(P\) и \(R\), чтобы получить треугольник \(PRQ\).

Согласно теореме о подобии треугольников, треугольники \(ABC\) и \(PRQ\) подобны, так как у них соответствующие стороны пропорциональны, а углы равны. Это можно показать следующим образом:

\(\frac{DP}{DA} = \frac{DQ}{DC} = \frac{DR}{DB} = k\)

Здесь \(k\) — коэффициент пропорциональности, который равен \(\frac{2}{3}\), так как точка \(O\) делит медианы в отношении \(1:2\).

Таким образом, сечение тетраэдра плоскостью, параллельной грани \(ABC\), является треугольником \(PRQ\), подобным треугольнику \(ABC\).

б) Найдем отношение площадей сечения \(PRQ\) и треугольника \(ABC\).

Используя формулу для вычисления площади треугольника через две стороны и угол между ними, получаем:

\(\frac{S_{PRQ}}{S_{ABC}} = \frac{PR \cdot PQ \cdot \sin \angle RPQ}{AB \cdot AC \cdot \sin \angle BAC} = \frac{1}{k^2} = \frac{9}{4}\)

Таким образом, отношение площадей сечения \(PRQ\) и треугольника \(ABC\) равно \(\frac{9}{4}\).