ГДЗ по Геометрии 10 класс Номер 73 Атанасян — Подробные Ответы

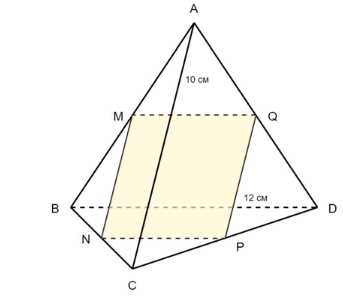
В тетраэдре \(ABCD\) точки \(M\), \(N\) и \(Р\) являются серединами рёбер \(АВ\), \(ВС\) и \(CD\), \(AC = 10\) см, \(BD = 12\) см. Докажите, что плоскость \(MNP\) проходит через середину \(К\) ребра \(AD\), и найдите периметр четырёх- угольника, получившегося при пересечении тетраэдра с плоско- стью \(MNP\).

В тетраэдре \(ABCD\) точки \(M\), \(N\) и \(P\) являются серединами рёбер \(AB\), \(BC\) и \(CD\) соответственно. Известно, что \(AC = 10\) см и \(BD = 12\) см. Докажем, что плоскость \(MNP\) проходит через середину \(Q\) ребра \(AD\), и найдём периметр четырёхугольника \(MNPQ\).

Поскольку \(MN\) является средней линией треугольника \(ABC\), она параллельна \(AC\). Согласно признаку параллельности прямой и плоскости, \(MN\) параллельна плоскости \(MNP\). Плоскость \(ACD\) пересекает плоскость \(MNP\) по прямой \(QP\), поэтому \(AC\) параллельна \(QP\). Так как \(P\) — середина ребра \(CD\), \(QP\) является средней линией треугольника \(ACD\), следовательно, \(Q\) — середина ребра \(AD\), а \(MQ\) — средняя линия треугольника \(ABD\).

Четырёхугольник \(MNPQ\) является параллелограммом, так как противоположные стороны \(MQ\), \(NP\) и \(MN\), \(QP\) параллельны. Периметр параллелограмма \(MNPQ\) вычисляется по формуле:
\[P_{\text{MNPQ}} = 2MQ + 2PQ = 2 \cdot \frac{BD}{2} + 2 \cdot \frac{AC}{2} = BD + AC = 22\text{ см}\]

Доказательство:
Рассмотрим точку \(Q\) — середину ребра \(AD\) тетраэдра \(ABCD\). Известно, что \(MN\) — средняя линия треугольника \(ABC\), следовательно, \(MN\) параллельна \(AC\). Согласно признаку параллельности прямой и плоскости, \(MN\) параллельна плоскости \(MNP\).

Плоскость \(ACD\) проходит через прямую \(AC\), параллельную плоскости \(MNP\), и пересекает её по прямой \(QP\). Таким образом, \(AC\) параллельна \(QP\). Так как \(P\) — середина ребра \(CD\), то \(QP\) является средней линией треугольника \(ACD\). Следовательно, \(Q\) является серединой ребра \(AD\), а \(MQ\) — средней линией треугольника \(ABD\).

Нахождение периметра четырёхугольника \(MNPQ\):
Докажем, что четырёхугольник \(MNPQ\) является параллелограммом. Известно, что \(MQ\) и \(NP\) параллельны \(BD\), так как являются средними линиями треугольников \(ABD\) и \(BCD\) соответственно. Аналогично, \(MN\) и \(QP\) параллельны, так как являются пересечениями плоскости \(ACD\) с гранями \(DAB\) и \(DBC\) соответственно. Таким образом, противоположные стороны четырёхугольника \(MNPQ\) параллельны, следовательно, он является параллелограммом.

Тогда периметр параллелограмма \(MNPQ\) можно найти по формуле:
\[P_{\text{MNPQ}} = 2MQ + 2PQ\]
Известно, что \(MQ\) равна половине ребра \(BD\), как средняя линия треугольника \(ABD\), и \(PQ\) равна половине ребра \(AC\), как средняя линия треугольника \(ACD\). Таким образом:
\[P_{\text{MNPQ}} = 2 \cdot \frac{BD}{2} + 2 \cdot \frac{AC}{2} = BD + AC = 22\text{ см}\]