
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 71 Атанасян — Подробные Ответы
Изобразите тетраэдр \(DABC\) и на рёбрах \(DB\), \(DC\) и \(ВС\) отметьте со- ответственно точки \(М\), \(N\) и \(К\). Постройте точку пересечения: а) прямой \(MN\) и плоскости \(АВС\); б) прямой \(КИ\) и плоскости \(ABD\).
Через середины рёбер \(AB\) и \(BC\) тетраэдра \(SABC\) проведена плоскость параллельно ребру \(SB\). Согласно теореме о параллельности прямых, пересекающих две параллельные плоскости, линии пересечения этой плоскости с гранями \(SAB\) и \(SBC\) будут параллельны ребру \(SB\).
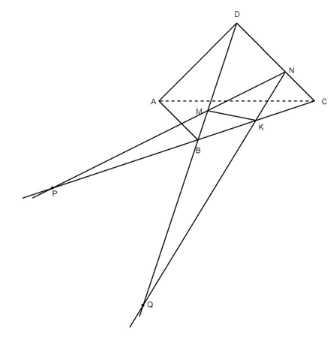
Для построения точек пересечения прямых \(MN\) и \(KN\) с плоскостями \(ABC\) и \(ABD\) соответственно, выполним следующие действия:
Рассмотрим треугольник \(ABC\) и прямую \(MN\), которая не параллельна плоскости \(ABC\). Продлим прямую \(MN\) до пересечения с плоскостью \(ABC\) в точке \(P\). Эта точка \(P\) является точкой пересечения прямой \(MN\) и плоскости \(ABC\).
Аналогично, для треугольника \(ABD\) и прямой \(KN\), которая не параллельна плоскости \(ABD\), продлим прямую \(KN\) до пересечения с плоскостью \(ABD\) в точке \(Q\). Эта точка \(Q\) является точкой пересечения прямой \(KN\) и плоскости \(ABD\).
Таким образом, точки \(P\) и \(Q\) являются искомыми точками пересечения прямых \(MN\) и \(KN\) с плоскостями \(ABC\) и \(ABD\) соответственно.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!