
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 68 Атанасян — Подробные Ответы
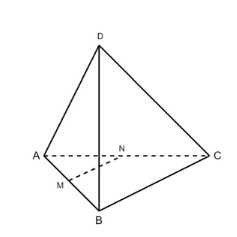
Точки \(M\) и \(N\) — середины рёбер \(AB\) и \(AC\) тетраэдра \(ABCD\). Докажите, что прямая \(MN\) параллельна плоскости \(BCD\).
Для доказательства параллельности прямой \(MN\) и плоскости \(BCD\) тетраэдра \(ABCD\) используем два утверждения.
Сначала рассмотрим прямые \(AB\) и \(CD\). Они пересекают прямую \(MN\) и образуют с ней равные накрест лежащие углы. Так как \(M\) и \(N\) — середины рёбер \(AB\) и \(AC\), то \( \angle AMN = \angle CND \). Это означает, что прямые \(AB\) и \(CD\) параллельны.
Далее рассмотрим плоскости \(ABC\) и \(BCD\). Они пересекают плоскость \(MNQ\) по параллельным прямым \(AB\) и \(CD\). Таким образом, плоскости \(ABC\) и \(BCD\) также параллельны.
В итоге, прямая \(MN\) параллельна плоскости \(BCD\) тетраэдра \(ABCD\).
Для доказательства параллельности прямой \(MN\) и плоскости \(BCD\) тетраэдра \(ABCD\) воспользуемся следующими утверждениями:
1. Если две прямые пересекают третью прямую и образуют с ней равные накрест лежащие углы, то эти две прямые параллельны.
2. Если две плоскости пересекают третью плоскость по параллельным прямым, то эти две плоскости параллельны.
Рассмотрим прямые \(AB\) и \(CD\). Они пересекают прямую \(MN\) и образуют с ней равные накрест лежащие углы, так как \(M\) и \(N\) — середины рёбер \(AB\) и \(AC\) соответственно. Следовательно, прямые \(AB\) и \(CD\) параллельны.
Теперь рассмотрим плоскости \(ABC\) и \(BCD\). Они пересекают плоскость \(MNQ\) по параллельным прямым \(AB\) и \(CD\). Следовательно, плоскости \(ABC\) и \(BCD\) параллельны.
Таким образом, мы доказали, что прямая \(MN\) параллельна плоскости \(BCD\) тетраэдра \(ABCD\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!